Как приготовить торт «Цифра»? Три проверенных рецепта и шаблоны для коржей
Сложность – 2 из 5, эффектность – 100 из 100! Кондитерским трендом 2018 года по праву можно назвать торт (а по мнению некоторых кондитеров – тарт) в виде цифры, буквы или символа (например, сердца). Считается, что идейным вдохновителем такого десерта стала кондитер из Израиля Adi Klinghofer.
Главные отличительные черты такого торта – четкость формы, гармоничное сочетание лаконичности и праздничности. Конструкция десерта донельзя проста: два коржа (это для классического варианта, но в сети уже попадаются фото этого десерта и с тремя коржами), и крем, отсаженный через кондитерский мешок с помощью насадки «Трубочка». Крем служит прослойкой между коржами, а также украшает верхний слой. Между капельками крема можно также отсадить конфитюр, чтобы придать еще одну нотку вкуса. Оформление при этом может быть любым: всё ограничивается лишь фантазией и возможностями кондитера. Для декора подойдут как живые, так и мастичные или вафельные цветы, меренга, маршмеллоу, зефир, макаронс, кондитерская посыпка, ягоды и кусочки фруктов – в общем, что ваша душа пожелает!
Очень важно, чтобы тесто получилось достаточно мягким, но при этом хорошо держало форму и не крошилось. Немаловажное значение имеет и крем: он должен хорошо пропитать коржи и при этом не «поплыть» и удержать декор. Можно использовать масляный крем, крем-чиз или на основе взбитого ганаша.
Немаловажное значение имеет и крем: он должен хорошо пропитать коржи и при этом не «поплыть» и удержать декор. Можно использовать масляный крем, крем-чиз или на основе взбитого ганаша.
Как вырезать такие ровные цифры?
Чтобы еще больше облегчить вам работу над таким тортом, мы приготовили для вас шаблоны в виде сердца и цифр, которые вы можете скачать абсолютно бесплатно вот здесь: все цифры и сердце одним архивом, весь русский алфавит одним архивом, сердце, звезда 21 см, звезда 26 см, цифра 0, цифра 1, цифра 2, цифра 3, цифра 4, цифра 5, цифра 6 и 9, цифра 7, цифра 8, цифра 8 толстенькая, цифра 0 толстенькая, цифра 1 толстенькая, цифра 2 толстенькая, цифра 3 толстенькая, цифра 4 толстенькая.
Все трафареты оптимизированы для печати на формате А4. Вам остается только распечатать их, вырезать из листа бумаги, приложить к раскатанному пласту теста и аккуратно вырезать корж по шаблону.
Если же хочется ещё более простой вариант, выбирайте готовые многоразовые трафареты.
А теперь перейдем к рецептам торта цифры!
Рецепт с пряничным тестом
Ингредиенты для коржей:
- 190 г муки
- 80 г сахара
- 50 г сливочного масла
- 1 яйцо
- 40 г меда
- ½ ч.л. соды
- щепотка соли
Приготовление коржей:
В сотейнике смешать сахар, яйцо, мед, соль. Перемешать до однородной массы. Добавить масло. Поставить сотейник на средний огонь. Постоянно помешивая, довести смесь до кипения. Снять с огня и добавить соду, перемешать. Масса должна увеличиться в объеме. Подождать, пока смесь остынет до комнатной температуры. После этого добавить половину просеянной муки и перемешать до однородной массы. Другую половину муки высыпать на рабочую поверхность. Вымесить тесто руками. Завернуть его в пакет и убрать в холодильник часа на 2 (можно на ночь).
После того, как тесто охладится, разделить его на 2 части и раскатать в пласт толщиной 3-4 мм. Тесто подпылить мукой, положить сверху трафарет и вырезать нужную цифру. Снять трафарет, убрать излишки теста. Заготовку наколоть вилкой, чтобы при выпечке тесто не пузырилось. Выпекать корж на тефлоновом коврике в разогретой до 170°С духовке до легкого румянца. Оставить корж остывать (сначала на коврике, потом переложить на решетку).
Ингредиенты для крема:
Приготовление крема:
Сливки довести до кипения, но не кипятить. Залить шоколад горячими сливками, хорошо перемешать и пробить блендером. Ганаш накрыть вплотную пищевой пленкой и убрать на холод часов на 8 (или на ночь). По истечении этого времени сыр взбить миксером до однородного мягкого состояния. Влить холодный ганаш и взбить на высокой скорости. Переложить крем в кондитерский мешок с насадкой «Трубочка».
Ингредиенты для малинового конфитюра:
- 100 г малинового пюре
- 1 ст.
 л. сахара
л. сахара - 1 ч.л. кукурузного крахмала
Приготовление конфитюра:
Сахар смешать с крахмалом и соединить с холодным пюре. Перемешать до однородного состояния. Поставить миску на средний огонь. Постоянно помешивая, кипятить 1-2 минуты. Дать конфитюру остыть, после чего переложить его в кондитерский мешок.
Сборка торта:
Крем отсадить «каплями» или «куполами» на первый корж. Между кремом отсадить конфитюр. Аккуратно накрыть вторым коржом и отсадить на него крем. Украсить по своему вкусу цветами, меренгой, маршмеллоу и т.п.
Рецепт с миндальным тестом
Ингредиенты для коржей (1 вариант):
Ингредиенты для крема:
- 400 г творожного сыра
- 250-350 г (можно 400 г) сливок 33%
- 170-220 г сахарной пудры по вкусу
Приготовление коржей:
Холодное сливочное масло порубить на кусочки при помощи ножа. В емкость с маслом добавить просеянную сахарную пудру, соль, миндальную и обычную муку. Все сухие ингредиенты перед добавлением в песочное тесто лучше просеять. Ножом порубить тесто до получения крошки (либо руками). К тщательно вымешанному и порубленному тесту добавить яйцо и желток. Быстро замешать эластичное тесто.
В емкость с маслом добавить просеянную сахарную пудру, соль, миндальную и обычную муку. Все сухие ингредиенты перед добавлением в песочное тесто лучше просеять. Ножом порубить тесто до получения крошки (либо руками). К тщательно вымешанному и порубленному тесту добавить яйцо и желток. Быстро замешать эластичное тесто.
Готовое песочное тесто Сабле разделить на 4 части, раскатать (после раскатки, тесто можно убрать в морозильник на 5 минут) и вырезать на пергаменте или на силиконовом коврике с помощью трафарета цифры. Выпекать в разогретой до 170°С духовке 10-15 минут.
Приготовление крема:
Соединить все ингредиенты (сливки налейте не все, чтобы контролировать желаемую консистенцию крема). Взбить миксером 2-3 минуты. Выложить крем в кондитерский мешок с насадкой «Трубочка» 8-12 мм в диаметре.
Сборка торта:
Отсадить крем по поверхности цифры. Накрыть вторым коржом. Снова отсадить крем. Можно добавить на каждый слой ягод и фруктов.
Если нет миндальной муки можно попробовать второй рецепт коржей.
Ингредиенты для коржей (2 вариант):
- 190 г сливочного масла
- 230 г сахара
- 400 г пшеничной муки
- 2 яйца
- 70 г сметаны
- 1 ч.л. разрыхлителя
Смешать размягченное сливочное масло с сахаром. К масляно-сахарной смеси добавить яйца и тщательно вымесите основу для песочного теста. Влить в тесто сметану. Добавить к песочному тесту просеянную муку, тщательно вымешивая его после каждой порции. Готовое песочное тесто должно быть эластичное и не липнуть к рукам.
Далее действуем, как в первом варианте.
Рецепт с песочным тестом
Ингредиенты для песочного теста сабле:
Приготовление коржей:
Просеять сухие ингредиенты. Миксером с помощью насадки «весло» взбить масло с сахарной пудрой. Добавить яйцо, перемешать. Добавить желток, перемешать. Добавить муку, замесить тесто. Разделить его на 2 части, обернуть плёнкой и убрать в холодильник минимум на 1 час (можно на ночь). Затем раскатать тесто толщиной около 3 мм. Припылить мукой, положить сверху трафарет и вырезать нужную букву (надо сделать по 2 варианта каждого символа). Заготовки отправить в морозилку на 10 минут. После этого выпекать в разогретой до 175°С духовке до золотистого цвета.
Добавить яйцо, перемешать. Добавить желток, перемешать. Добавить муку, замесить тесто. Разделить его на 2 части, обернуть плёнкой и убрать в холодильник минимум на 1 час (можно на ночь). Затем раскатать тесто толщиной около 3 мм. Припылить мукой, положить сверху трафарет и вырезать нужную букву (надо сделать по 2 варианта каждого символа). Заготовки отправить в морозилку на 10 минут. После этого выпекать в разогретой до 175°С духовке до золотистого цвета.
Ингредиенты для крема «Дипломат»:
- 320 мл молока
- стручок ванили
- 90 г сахара
- 30 г сливочного масла
- 50 г кукурузного крахмала
- 2 яйца
- 300 г сливок 33%
- 8 г желатина
- 50 г воды
Приготовление крема:
Смешать венчиком 45 г сахара и крахмал. Добавить яйца и немного молока. Перемешать до однородности. Замочить желатин в воде.:max_bytes(150000):strip_icc()/NUMBERS-01-56a80f0c5f9b58b7d0f045d3.png) Разогреть молоко с ванилью и оставшимся сахаром. Тонкой струйкой ввести в яичную смесь, всё время помешивая венчиком. Вернуть смесь на малый огонь. Довести до кипения, постоянно помешивая. Снять с огня, добавить масло, размешать. Растворить на горячей водяной бане желатин. Влить его в крем, размешать (смотрите, чтобы не было комочков). Накрыть крем пищевой пленкой в контакт, остудить до комнатной температуры. Когда крем остынет, взбить холодные сливки и частями ввести в заварной крем, предварительно взбитый миксером. Переложить крем в кондитерский мешок с насадкой «Трубочка».
Разогреть молоко с ванилью и оставшимся сахаром. Тонкой струйкой ввести в яичную смесь, всё время помешивая венчиком. Вернуть смесь на малый огонь. Довести до кипения, постоянно помешивая. Снять с огня, добавить масло, размешать. Растворить на горячей водяной бане желатин. Влить его в крем, размешать (смотрите, чтобы не было комочков). Накрыть крем пищевой пленкой в контакт, остудить до комнатной температуры. Когда крем остынет, взбить холодные сливки и частями ввести в заварной крем, предварительно взбитый миксером. Переложить крем в кондитерский мешок с насадкой «Трубочка».
На каждую букву нанести крем, аккуратно положить второй корж и покрыть его кремом. Украсить по своему усмотрению сладостями, ягодами и т.п. Убрать торт в холодильник на 12 часов, чтобы он хорошо пропитался.
Несколько советов:
- Собирать торт лучше сразу на подложке и коробке, в которой вы будете его переносить.
- Если при украшении использовать безе, то их нужно хорошо высушить, иначе они могут размягчиться от крема.

- При украшении живыми цветами не забывайте изолировать стебли, чтобы они не соприкасались с продуктом. Это можно сделать с помощью шоколада или специальной тейп-ленты.
Такие тортики могут быть не только в виде цифр, но и букв, например, инициалов именинника или даже его имени. Кроме того, в предстоящие праздники наверняка будут популярны такие десерты в виде сердца.
Напоминаем, бесплатно скачать шаблоны для таких тортиков вы можете по ссылкам в начале статьи, а видео по сборке такого торта смотрите в нашем профиле в Инстаграм – @ellecraftstore.
Удачи!
При подготовке и публикации статьи использовались материалы из открытых источников: сайта sugargeekshow.com, а также профилей в Инстаграм @adikosh223, @yuliya_small и @ilzi_
шаблоны для вырезания цифры
Шаблоны цифр
У нас вы сможете скачать цифры от 0 до 9. Шаблоны цифр представлены в нескольких вариантах с использованием разнообразных шрифтов. Использовать такие трафареты цифр можно при подготовке к урокам математики, алгебры, физики, химии, геометрии и другим предметам. Для оформления плакатов, стенгазет, чертежей, докладов всегда применяют шаблоны с цифрами.
Использовать такие трафареты цифр можно при подготовке к урокам математики, алгебры, физики, химии, геометрии и другим предметам. Для оформления плакатов, стенгазет, чертежей, докладов всегда применяют шаблоны с цифрами.
Но трафареты могут пригодится не только в школе или детском саду. Какой-либо декор, роспись на стене, написание шифра или кода, начертание схем и карт, построение лекал не получится сделать без использования шаблонов.
Трафареты с цифрами очень эффективно используют для обучения дошкольников счету и математики и развития у них математического мышления, логики и памяти. Распечатанные цифры нужно вырезать, приклеить к картонным карточкам и регулярно заниматься с ребенком счетом.
Если у вас нет возможности распечатать шаблоны, приложите лист бумаги к монитору, перерисуйте изображение, а затем перенесите его на плотный картон.
Данные шаблоны цифр можно использовать для печати, вырезания из бумаги или фетра, как трафарет, выкройку или раскраску.:max_bytes(150000):strip_icc()/NUMBERS-07-56a80f0e3df78cf7729bc1f7.png)
Они отлично подойдут для создания забавных коллажей, праздничных плакатов на детские утренники, а также для обучения детей счёту.
Как сделать трафареты цифр своими руками?
Очень часто нам приходится готовить объявления, плакаты, аппликации, где участвуют цифры. Сделать это своими руками без помощи трафаретов бывает сложно. На нашем сайте мы предлагаем трафареты цифр для вырезания от 1 до 9, которые можно скачать бесплатно. Трафарет необходимо распечатать, чтобы использовать в работе.
Отдельные цифры
Цифры общим списком
Где их можно применить?
Во-первых, трафареты цифр от 1 до 9 будут полезны учителям и воспитателям детских учреждений, которым часто приходится готовить различные стенгазеты, печатные объявления, плакаты своими руками. При наличии трафаретов для вырезания это будет несложно сделать. Стоит только скачать трафарет, распечатать, приложить к основе, обвести и вырезать.:max_bytes(150000):strip_icc()/NUMBERS-04-56a80f0d3df78cf7729bc1ea.png) Особенно трудной для написания является цифра 8: ее легко изготовить с помощью трафарета. Итак, цифры готовы.
Особенно трудной для написания является цифра 8: ее легко изготовить с помощью трафарета. Итак, цифры готовы.
Трафареты цифр от 1 до 9 могут весьма помочь школьникам. Нетрудно будет с их помощью вырезать и цифру 8.
Школьникам также приходится много делать своими руками: готовить праздничные выступления, оформления для концертных залов, просто поделки из бумаги. Трафарет может помочь им в нужную минуту. Стоит только скачать трафареты с нашего сайта.
Полезными будут трафареты для вырезания цифр от 1 до 9 и для детских садов и развивающих детских центров. При подготовке к школе дети изучают цифры от 1 до 10. Воспитатель может предложить ребятам сделать цифры своими руками. Для этого воспитатель должен скачать трафарет, распечатать и предложить его детям. Дети обводят его на обратной стороне цветной бумаги и вырезают. Можно каждый раз вырезать изучаемую цифру или давать детям домашнее задание вырезать изученную цифру с помощью трафарета. Сделанные заготовки помогут детям в дальнейшем изучать десятки и сотни.
Процесс вырезания чрезвычайно полезен для запоминания дошкольниками самой формы цифры. Кроме того, отрабатывается мелкая моторика, дети становятся усидчивее, внимательнее. Так, если взять в качестве примера цифру 8, то получается, что запомнить ее легко, а вот вырезать довольно трудно. В цифре 8 придется дважды вырезать внутри контура, что требует особого внимания и аккуратности. Поэтому для детей, казалось бы, простая цифра 8 отнюдь не проста, если приходится ее вырезать с помощью трафарета.
И, конечно, не только воспитатели и учителя могут пользоваться трафаретными заготовками. Изучать с ребенком цифры, вырезая их из цветной бумаги или раскрашивая по контуру в разные цвета, могут и родители дома. Конечно, при этом требуется постоянный контроль за детьми, поскольку оставлять их наедине с ножницами нельзя. Но зато вы получите долгожданный результат. Вам, уважаемые родители, необходимо всего лишь скачать трафарет и распечатать его на бумаге. Затем предложите ребенку приложить цифру к цветной или белой бумаге, обвести по контуру и затем отрезать лишнее, чтобы в результате получилась цифра.:max_bytes(150000):strip_icc()/NUMBERS-05-56a80f0d3df78cf7729bc1ef.png) Увидите, в какой восторг приведет малыша возможность сделать цифру своими руками. Цифры вы выучите очень быстро, а полученные заготовки используйте для изучения математических действий, составляя из них примеры.
Увидите, в какой восторг приведет малыша возможность сделать цифру своими руками. Цифры вы выучите очень быстро, а полученные заготовки используйте для изучения математических действий, составляя из них примеры.
Таким образом, предложенные на нашем сайте трафареты цифр могут быть полезны как взрослым, так и детям. Особенно они могут помочь в развитии детей, если взрослые не поленятся поработать вместе с детьми над изготовлением цифр.
Шаблоны цифр и математических знаков
Для того, чтобы научить ребенка считать в уме, удобно использовать карточки с цифрами и математическими знаками.
Надо распечатать нескотолько комплектов карточек.
А дальше просто предложите «Давай, поиграем в школу».
Ребенок 3-4 лет еще не может быстро писать. А вот выкладывать примеры с помощью карточек, это ему под силу сделать быстро.
Скачать шаблоны цифр: 1-9.rar [119,1 Kb] (cкачиваний: 1525)
Шаблоны цифры для вырезания распечатать, русские цифры, римские цифры
Говорят, что цифры несут в себе особую магию. Их энергетику можно ощутить в окружающем нас пространстве, украшениях и оберегах. Трафарет представляет собой шаблон, который вырезают из пластика или плотной бумаги. При нанесении краски на верхнюю часть пластины, оттенок проникает сквозь отверстия, создавая требуемый шаблон на выбранной поверхности. Сегодня готовые трафареты производятся из прозрачного пластика, толщиной от 5 до 7 мм, с помощью компьютеризированного лазерного резака. Они гибкие, достаточно прочные и очень простые в использовании. Цифровые шаблоны можно сделать самому, распечатав их на картон с помощью принтера и вырезав нужные фрагменты.
Их энергетику можно ощутить в окружающем нас пространстве, украшениях и оберегах. Трафарет представляет собой шаблон, который вырезают из пластика или плотной бумаги. При нанесении краски на верхнюю часть пластины, оттенок проникает сквозь отверстия, создавая требуемый шаблон на выбранной поверхности. Сегодня готовые трафареты производятся из прозрачного пластика, толщиной от 5 до 7 мм, с помощью компьютеризированного лазерного резака. Они гибкие, достаточно прочные и очень простые в использовании. Цифровые шаблоны можно сделать самому, распечатав их на картон с помощью принтера и вырезав нужные фрагменты.
Содержание статьи
Как можно использовать шаблоны, на примере цифр 8 и 23
Граффити — быстрый и относительно простой метод уличного искусства. Он очень популярен из-за своей дешевизны. Для воссоздания цифрового шаблона необходим лишь кусок картона, нож и банки с краской.
Цифровые трафареты применяют:
- Для создания изделий с ровными, красивыми краями.
 Например, торт-цифра состоит из коржей, вырезанных по готовому шаблону. Его можно распечатать или начертить самому. На корж кладут трафарет и обрезают лишние края. Готовые восьмерки выпекают и украшают.
Например, торт-цифра состоит из коржей, вырезанных по готовому шаблону. Его можно распечатать или начертить самому. На корж кладут трафарет и обрезают лишние края. Готовые восьмерки выпекают и украшают.
- Для идентификации зданий и этажей.
Номерная табличка в средиземноморском стиле на мраморном фоне смотрится довольно оригинально.
- Цифрами украшают зал для проведения детского утренника. Например, в преддверии 23 февраля число вырезают из пенопласта и декорируют по краю подарочной лентой.
- Для создания фотозоны, где гости с удовольствием проведут время.
- Маркировку изделий проводят также при помощи цифр.
- Шаблон необходим для нанесения номерного знака на транспортное средство.
- Как развивающийся метод для моторики рук дошкольника.
- Как элемент декора мебели и одежды.
Трафарет цифры шаблоны, распечатать и вырезать:
В советские времена плакаты и стенгазеты зачастую оформляли с помощью специальных наборов трафаретов. В их состав входили цифры размером 15, 20 мм. Сегодня шаблоны нужного размера не всегда найдешь, да и стоимость их высока, поэтому мастерицы приловчились делать их из подручных материалов. Существует несколько способов изготовления трафарета:
В их состав входили цифры размером 15, 20 мм. Сегодня шаблоны нужного размера не всегда найдешь, да и стоимость их высока, поэтому мастерицы приловчились делать их из подручных материалов. Существует несколько способов изготовления трафарета:
- Шаблон из папки-скоросшивателя, толщиной 0,2 мм. Для работы пойдет только верхняя прозрачная часть. Ее разрезают на квадратики и крепят на мат для резки, а затем отправляют в плоттер – специальное устройство для проработки мелких деталей. Аппарат создает загруженный шаблон.
- На принтере распечатывают нужную цифру. Вырезают квадратик из прозрачной части папки и накладывают на рисунок. Все части фиксируют на поверхности скотчем. Острым наконечником паяльника (260 С) проходят по контурам изображения.
 Канцелярским ножом убирают погрешности.
Канцелярским ножом убирают погрешности. - Распечатывают картинку, обрезают концы и закрепляют ее на коврике. Сверху кладут клеенку и фиксируют заготовку скотчем. Вырезают необходимые детали крафт ножом.
- Из самоклеющейся пленки делают заготовку размером листа А4. Ее обязательно выравнивают. С изнанки распечатывают необходимое изображение и с помощью маникюрных ножниц удаляют лишние детали. Самоклейку снимают и используют за надобностью.
- Существует способ создания цифрового шаблона на основе собственного почерка. Для этого на листе А 4 пишут цифры и выводят на монитор через сканер, не забыв каждую цифру сделать отдельным файлом. Затем запускают программу FontCreator Program и создают шаблон.
красивые русские цифры
Красота понятие относительное, но главное при создании шаблона – это разборчивость, оригинальность и умение точно передать мысль.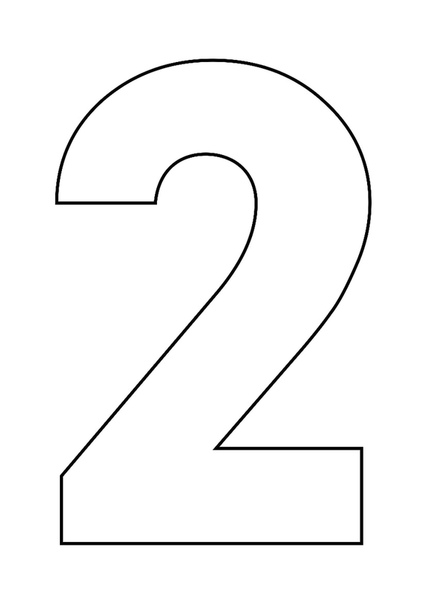 Конечно, лучше самому создать свой собственный трафарет, но, если приглянулся уже готовый макет из интернета, его также можно использовать (только помним об авторском праве). Есть масса бесплатных шаблонов, которые можно загрузить и применить для особого случая.
Конечно, лучше самому создать свой собственный трафарет, но, если приглянулся уже готовый макет из интернета, его также можно использовать (только помним об авторском праве). Есть масса бесплатных шаблонов, которые можно загрузить и применить для особого случая.
красивые римские цифры
Шаблоны римских цифр востребованы для оформления циферблата механических часов, определения группы крови, написания даты рождения (месяца) и других случаев. Чаще применяют все же русские цифры, но римские трафареты также оригинальны и красивы.
красивые трафареты римских цифр от 1 до 12, для оформления часов
Приведенный ниже трафарет (диаметр 12,5 см) подходит для многоразового нанесения краски на поверхность. Образец выполнен в привычном стиле.
Размер блока — 18 х 26 см, высота цифр — 3 см.
Следующий образец выполнен в декоративном стиле шрифта Monti-Decor_A.
Шаблон в романтично-весеннем стиле.
красивые цифры для вырезания от 0 до 9
Шаблоны цифр от 0 до 9 поданы в нескольких вариантах.:max_bytes(150000):strip_icc()/NUMBERS-03-56a80f0c5f9b58b7d0f045db.png) Здесь применены разнообразные замысловатые шрифты. Их можно скачать и распечатать, а при отсутствии принтера — приложить лист к экрану и скопировать цифры на бумагу, а затем перенести на картон. Трафареты подходят для перенесения на фетр, для раскраски и оформления зала.
Здесь применены разнообразные замысловатые шрифты. Их можно скачать и распечатать, а при отсутствии принтера — приложить лист к экрану и скопировать цифры на бумагу, а затем перенести на картон. Трафареты подходят для перенесения на фетр, для раскраски и оформления зала.
красивые цифры для детей
Детские цифровые шрифты пригодятся для украшения зала к празднику и создания коллажей.
Их подготовку часто проводят совместно с детьми. Таким способом можно не только развить моторику детских ручек, но и попутно познакомить со счетом.
Детский шрифт отличается веселостью и озорством. Здесь уместны глазки, реснички, звездочки и цветочки.
красивые цифры для праздников
Первое, что бросается в глаза нашим гостям во время любого торжества — это оригинальное оформление зала. Здесь не обойтись без объемных цифр, украшенных лентами, цветами, бусинками и даже пуговицами. Полет фантазии в таких случаях многогранен.
Красивые цифры на праздник – это не только украшение стола, но и необычная фотозона.
Праздничная цифра из картона, которая декорирована цветами и листьями.
Для празднования юбилея свадьбы, например, 40-й годовщины родителей, оригинально смотрится вот такой приятный сюрприз. Для его создания понадобятся черно-белые фотографии, картонная коробка и двухсторонний скотч.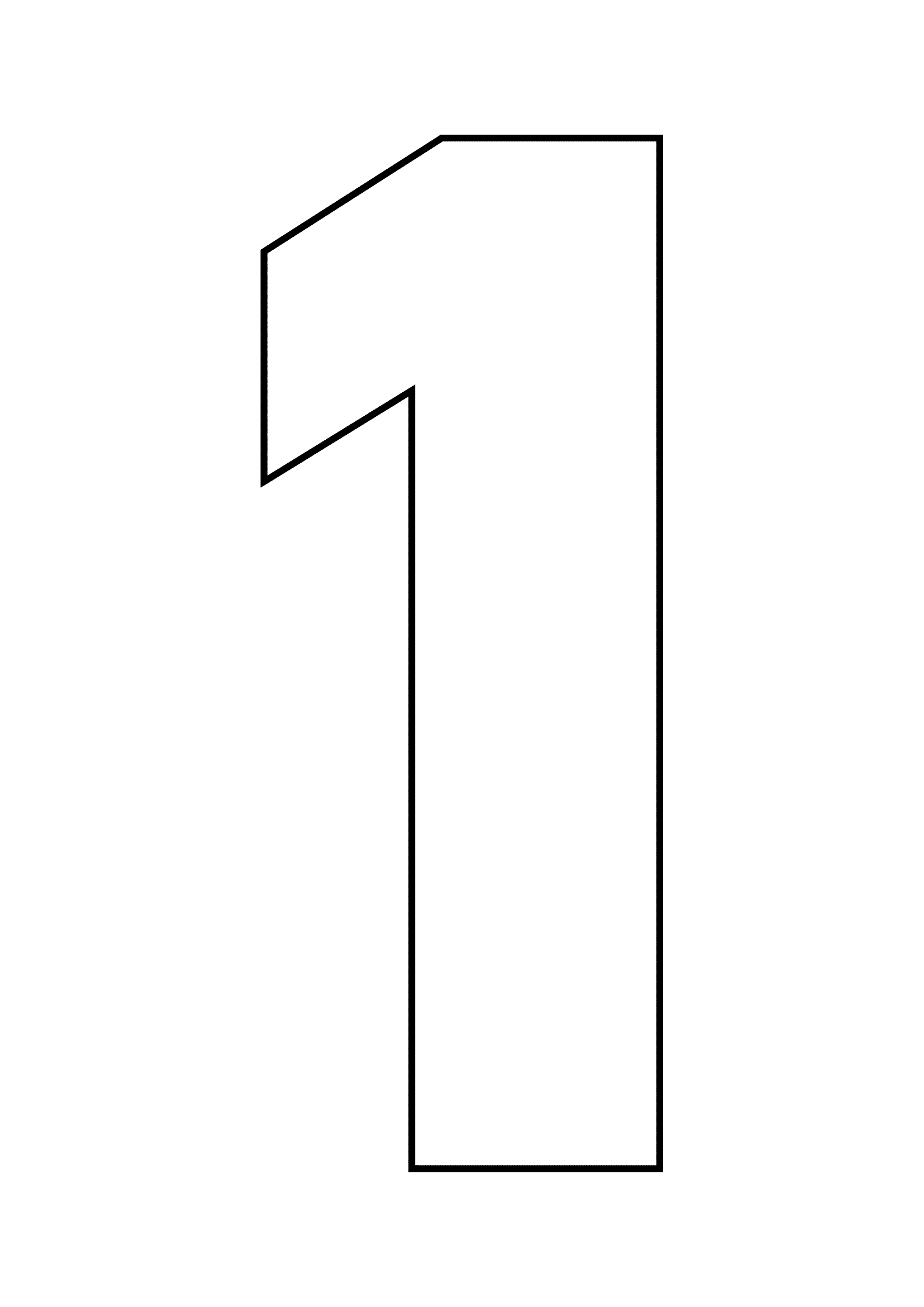 Из картона вырезают основу для цифр, на которую скотчем крепят фотографии сцен семейной жизни.
Из картона вырезают основу для цифр, на которую скотчем крепят фотографии сцен семейной жизни.
Цифра, украшенная круглыми цветами, выглядит нежно и нарядно.
Праздничное оформление зала для 6-летия девочки не обойдется без главной цифры, декорированной красной лентой.
Объемная цифра для детского праздника с сюрпризом.
красивые цифры на день рождения
Праздник дарит нашим деткам незабываемые минуты. Они окружены особым вниманием со стороны родных и гостей.
Первый шаг, первое слово и, конечно же, первый день рождения! Он, безусловно, более значимый для родителей, нежели для самого ребенка. Здесь необходимо учесть все: планирование стола, круг приглашенных гостей и украшение зала. Объемные единички делаются быстро и просто, главное -запастись картоном, лентами и клеем.
Второй вариант представлен цифрой с бахромой размером 80 см. Ее можно подарить имениннику, водрузить на стол или фотографироваться с ней.
Цифра со звездами для звездного героя и принцессы.:max_bytes(150000):strip_icc()/NUMBERS-06-56a80f0d5f9b58b7d0f045e4.png)
Многие люди считают, что устраивать вечеринки по случаю дня рождения детей в возрасте до 4 лет — пустая трата денег и времени. Малыши вряд ли способны запомнить праздник и правильно вести себя за столом. Тем не менее, дни рождения очень важны для всех возрастов. Ребенок сможет встретиться и поиграть с другими детьми, а также получить от этого массу удовольствия. А вот с такими фотозонами его снимки будут незабываемыми.
Цифра 2 (размер 30 х 40 см) с лентами и жемчужинами
- гофр картон,
- двусторонний скотч,
- степлер,
- ножницы,
- атласная лента (6-7 м, ширина 5 см),
- бусины.
Работа займет около часа. Картон из старой коробки будет служить основой двойки. Сначала вырезают шаблон цифры, для прочности проклеивают две одинаковые заготовки. Ленту закрепляют степлером или скотчем, концы прячут. Бусины фиксируют термопистолетом или пришивают.
Цифра 2 декорирована фрагментами цирковых представлений.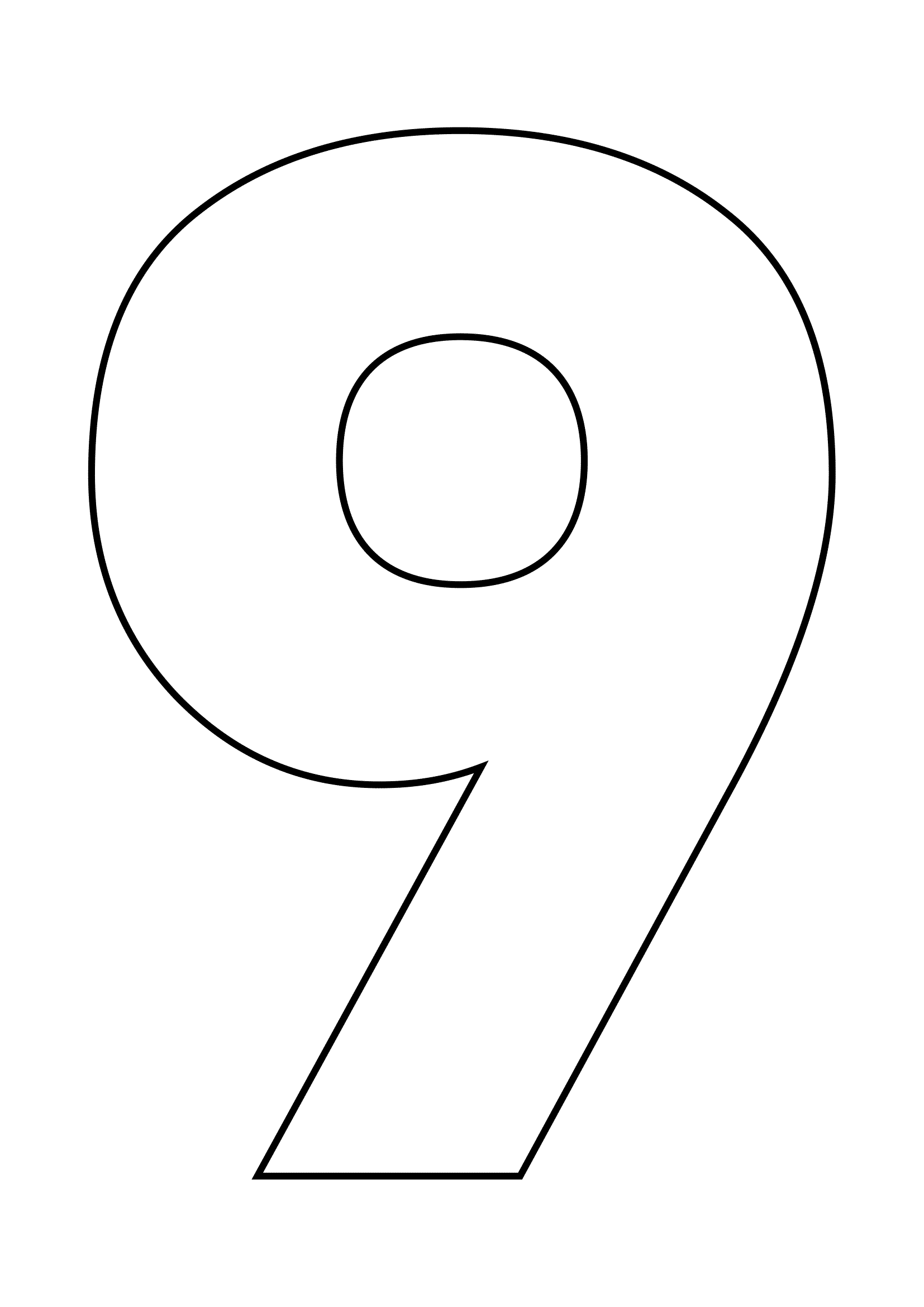
Для третьей годовщины праздничную цифру можно вырастить в цветочном горшке.
- цветочный горшок,
- картон,
- деревянные шпажки,
- камушки,
- атласная лента (0,5 см и 3,5 см),
- термопистолет.
Из картона делают две заготовки для цифры, а затем их проклеивают. К низу крепят две шпажки, на которых конструкция будет стоять в горшке. Обматывают заготовку лентами, края фиксируют клеем.
Горшок заполняют камушками и отправляют внутрь цифру. На ее краях можно пришить атласные розочки.
Не стоит покупать готовые цифры, ведь их всегда можно смастерить из подручных материалов.
Удачно организованный праздник для 4-х летнего малыша отличается простотой и непринужденной обстановкой.
Цифру 4 можно смастерить в тон платья именинницы. Ее украшают бумажными ромашками и декоративными коровками.
А настоящему супермену делают соответствующее число.:max_bytes(150000):strip_icc()/NUMBERS-09-56a80f0e5f9b58b7d0f045f2.png)
В пять лет дети обычно говорят о своих пожеланиях касательно проведения предстоящего торжества. Здесь не обойтись без воздушных шаров, декоративных цветов и объемных цифр.
Праздничное настроение в интерьер внесет пятерка из креповой бумаги. На число размером 50 см потребуется около 3-х свертков бумаги, картон и клеевой пистолет.
Цветы делают из квадратов, которые в центре накручивают на кончик карандаша. Их крепят к основе клеем.
После праздника цифровой декор можно повесить на стену именинника и оставить до следующего года.
Для зимнего праздника пятерку покрывают голубой бумагой и присыпают слой клея мишурой. Ее устанавливают на шпажку в прозрачную вазу.
Для шестого дня рождения можно приготовить цифру из набитых гвоздей и переплетения ярких нитей.
Седьмой день рождения может пройти в окружении сладостей.
как красиво распечатать цифру 8
Восьмерку можно применить для многих случаев: на женский праздник, день рождения, для декора мебели и одежды. Здесь вариантов может быть множество – от строгих черно-белых шаблонов до объемных чисел, декорированных цветами, бусинами и даже пуговицами.
Здесь вариантов может быть множество – от строгих черно-белых шаблонов до объемных чисел, декорированных цветами, бусинами и даже пуговицами.
Строгие варианты
Весенний вариант с бахромой.
красивые цифры 23 февраля
23 февраля – чисто мужской праздник, а вот приготовится к нему необходимо заранее. Вариантов декора здесь может быть несколько.
Конечно, оригинально выглядят надписи, выполненные в технике квиллинг или вырезанные канцелярским ножом.
цифры на красивом фоне
При оформлении композиции важно правильно выбрать фон, чтобы цифры не потерялись. Он также не должен быть кричащим.
Цифры дополняют и часто размещают на фоне сердец.
Дополнением к числам могут быть цветочные арки с шарами.
А также просто разбросанные или парящие гелевые шары.
Сказочные персонажи также удачно дополняют общую композицию с числами.
красивые цифры детские картинки
Особенностью детских шаблонов цифр могут быть шрифты-картинки. Числа иногда рисуют вместе со сказочными персонажами.
Для наглядности их дополняют глазами и геометрическими фигурами.
Глаза и машущие руки цифр обращают на себя внимание малыша.
красивая цифра 50
50-ти летний рубеж заставляет искать интересные идеи и изюминки для предстоящего праздника. Цифра 50 выполнена в двух оттенках: желтый – это нежность и ласка, которые юбиляр дарит окружающим, а красный символизирует активность и задор. Согласно шаблона делают две заготовки, одна из них по контуру на 2 см меньше другой. Первую обтягивают желтым велюром, а вторую – красным.
Вокруг второй цифры обходят золотистой лентой и накладывают ее на первую заготовку. Высота конструкции около 95 см.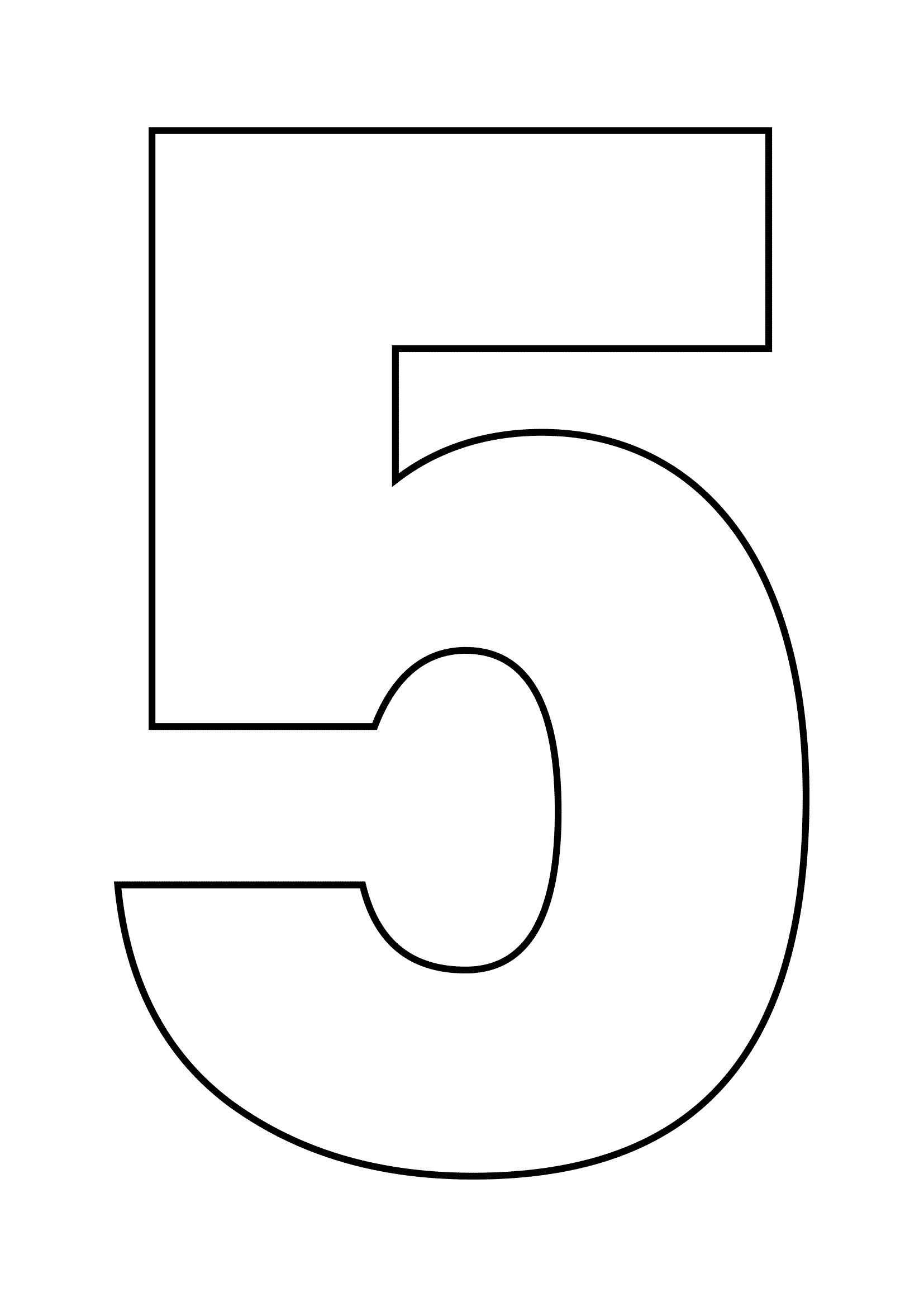
Торт-цифра
Цифра, декорированная цветами из бумажных салфеток.
красивая цифра 60
Этот возраст часто приходит с большим багажом знаний, финансовой стабильностью и большим количеством друзей.
Памятная цифра-коллаж из семейных фото.
Трогательный торт-цифра
красивая цифра 30
Шаблон из пенопласта, который можно превратить в настоящий шедевр при помощи цветов, велюра, лент и бусинок.
Цифра 30, оклеенная синим скотчем и декорированная рыбками и сеткой.
Юбилейное число, украшенное цветами из салфеток.
красивая цифра 25
Торт-цифра
Оригинальный шаблон для нанесения на футболку или кепку.
красивая цифра 18
Шаблон можно применить для декора молодежной футболки или сумки.
Для именинника готовят вот такое объемное число.
Номерная табличка с цифрой 18 может стать жанром искусства.
Как красиво украсить цифры
Смастерить цифры можно не только для детей, но и для взрослых. Достаточно продумать их оттенки, выбрать оригинальный шаблон и подарить вместе с букетом или прикрепить к подарочной коробке. Вариантов предостаточно.
Достаточно продумать их оттенки, выбрать оригинальный шаблон и подарить вместе с букетом или прикрепить к подарочной коробке. Вариантов предостаточно.
Главное — экспериментируйте, и тогда ваш памятный подарок обязательно окажется в центре внимания гостей и самого именинника.
Шаблоны ячеек на складе – Клеверенс
Последние изменения: 30.01.2019
Выберите уточнение:
Шаблоны ячеек удобны тем, что позволяют задать сразу большую группу ячеек и метод формирования названий и штрихкодов для них.
Это упрощает процесс (нам не требуется заводить вручную сотни ячеек) и значительно уменьшает расход памяти на мобильном терминале.
Шаблон штрихкода ячеек задается примерно такого вида:
99{параметр:число символов}{параметр: число символов}
99 – фиксированная часть (можно указывать не только цифры, но и буквы), может располагаться не только в начале, но и в середине шаблона штрихкода или в конце.
Параметр – номер, ряд, этаж, сектор и т.д.
Число символов – количество символов параметра.
Шаблон может состоять из одного или нескольких параметров 99{Ряд:2}{Номер:3}.
Шаблон имени для ячейки задается уже без указания длины каждой группы цифр параметра {Ряд}-{Номер}.
Штрихкод 9912548, означает: 99 – общее начало, 12 – ряд, номер – 548. При этом согласно шаблону имени, отображаемое название ячейки будет «12-548».
Примеры шаблонов штрихкодов ячеек
Пример 1 | Шаблон с одним параметром
Выгруженные данные:
|
Шаблон имени
|
Шаблон штрихкода
|
|
{Линия}
|
{Линия:2}
цифра «2» означает число символов штрихкода
|
|
{Стеллаж}
|
{Стеллаж:3}
цифра «3» означает число символов штрихкода
|
|
{Позиция}
|
{Позиция:5}
цифра «5» означает число символов штрихкода
|
Сканируемые (вводимые) данные:
Штрихкод: «32183»
Разбор по шаблону:
При вводе штрихкода ячейки «32183», будет производиться поиск подходящего шаблона.
{Линия:2} – шаблон не подходит, не совпадает количество символов в параметре
{Стеллаж:3} – шаблон не подходит, не совпадает количество символов в параметре
{Позиция:5} – шаблон подходит, совпадает количество символов в параметре
Результат:
В данном примере была выбрана ячейка по шаблону {Позиция:5}, потому что поиск велся по пяти символам штрихкода.
Пример 2 | Шаблон с фиксированной частью и несколькими параметрами
Выгруженные данные:
|
Шаблон имени
|
Шаблон штрихкода
|
|
99-{Линия}-{Стеллаж}
|
99{Линия:3}{Стеллаж:3}
99 – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
ПР-{Стеллаж}-{Позиция}
|
ПР{Стеллаж:3}{Позиция:3}
ПР – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
ПР-{Стеллаж}-{Позиция}
|
ПР{Стеллаж:3}{Позиция:5}
ПР – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
99-{Линия}-{Позиция}
|
99{Линия:3}{Позиция:5}
99 – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
Имена шаблонов могут совпадать, но иметь разные шаблоны штрихкода.
Сканируемые (вводимые) данные:
Штрихкод: «99321965»
Разбор по шаблону:
При вводе штрихкода ячейки «99321965», будет производиться поиск подходящего шаблона.
99{Линия:3}{Стеллаж:3} – шаблон подходит, совпадает фиксированная часть и количество символов в параметре
ПР{Стеллаж:3}{Позиция:3} – шаблон не подходит, не совпадает фиксированная часть
ПР{Стеллаж:3}{Позиция:5} – шаблон не подходит, не совпадает фиксированная часть количество символов в параметре
99{Линия:3}{Позиция:5} – шаблон не подходит, не совпадает количество символов в параметре
Результат:
В данном примере была выбрана ячейка по шаблону 99{Линия:3}{Стеллаж:3}, потому что поиск велся по восьми символам штрихкода, с фиксированной частью 99.
Пример 3 | Ячейка не найдена по шаблону
Выгруженные данные:
Выгруженные данные:
|
Шаблон имени
|
Шаблон штрихкода
|
|
99-{Линия}-{Стеллаж}
|
99{Линия:3}{Стеллаж:3}
99 – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
98-{Стеллаж}-{Позиция}
|
98{Стеллаж:3}{Позиция:3}
98 – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
ПР-{Стеллаж}-{Позиция}
|
ПР{Стеллаж:3}{Позиция:5}
ПР – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
99-{Линия}-{Позиция}
|
99{Линия:3}{Позиция:5}
99 – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
Сканируемые (вводимые) данные:
Штрихкод: «ПР321965»
Разбор по шаблону:
При вводе штрихкода ячейки «ПР321965», будет производиться поиск подходящего шаблона.
99{Линия:3}{Стеллаж:3} – шаблон не подходит, не совпадает фиксированная часть и количество символов в параметре
98{Стеллаж:3}{Позиция:3} – шаблон не подходит, не совпадает фиксированная часть
ПР{Стеллаж:3}{Позиция:5} – шаблон не подходит, не совпадает количество символов в параметре
99{Линия:3}{Позиция:5} – шаблон не подходит, не совпадает фиксированная часть и количество символов в параметре
Результат:
В данном примере к введенному штрихкоду не подходит ни один из выгруженных шаблонов ячеек. На терминале выведется надпись «неверный штрихкод ячейки» или «отсутствует в заявке» и будет предложено выбрать другую ячейку».
На терминале выведется надпись «неверный штрихкод ячейки» или «отсутствует в заявке» и будет предложено выбрать другую ячейку».
|
|
|
Пример 4 | Выбор шаблона из нескольких подходящих
Возможна такая ситуация, когда к отсканированному штрихкоду могут подходить несколько шаблонов.
Выгруженные данные:
|
Шаблон имени
|
Шаблон штрихкода
|
|
99-{Линия}-{Стеллаж}
|
99{Линия:3}{Стеллаж:3}
99 – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
99-{Стеллаж}-{Позиция}
|
99{Стеллаж:3}{Позиция:3}
99 – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
ПР-{Стеллаж}-{Позиция}
|
ПР{Стеллаж:3}{Позиция:5}
ПР – фиксированное начало, цифры после «:» означают количество символов в параметрах.
|
|
99-{Позиция}
|
99{Позиция:6}
99 – фиксированное начало, цифра «6» означают количество символов в параметре.
|
|
99321965
|
99321965 – шаблон ячейки фиксированный.
|
Сканируемые (вводимые) данные:
Штрихкод: «99321965»
Разбор по шаблону:
При вводе штрихкода ячейки «99321965», будет производиться поиск подходящего шаблона.
99{Линия:3}{Стеллаж:3} – шаблон подходит
99{Стеллаж:3}{Позиция:3} – шаблон подходит
ПР{Стеллаж:3}{Позиция:5} – шаблон не подходит, не совпадает фиксированная часть и количество символов в параметре
99{Позиция:6} – шаблон подходит
99321965 – шаблон подходит
Результат:
В данном примере к введенному штрихкоду подходят несколько шаблонов. Будет выбран шаблон 99{Линия:3}{Стеллаж:3}.
Будет выбран шаблон 99{Линия:3}{Стеллаж:3}.
Если к штрихкоду подходят несколько шаблонов, то из них выбирается тот, который находится в списке первым.
В шаблонах ячеек можно использовать регулярные выражения. Примеры шаблонов ячеек с регулярными выражениями смотрите в статье Использование регулярных выражений в шаблонах штрихкодов.
Была ли статья полезна?
Игрушки из фетра своими руками
Доброго дня дорогие рукодельницы или просто читатели!
Сегодня я хочу поделиться новыми интереснейшими идеями для творчества.
У меня недавно случилась долгожданная радость! К нам в гости приехала моя родная сестра с племянником которому уже один годик, а мы его увидели в живую первый раз, так как живут они от нас очень далеко (4 дня на поезде ехали).
И мне конечно же захотелось сделать моему любимому племяшке какой нибудь полезный подарок. В магазинах полно всего, полки ломятся от товаров, но это все не то. В них нет какой то индивидуальности, да и производство одно китайское в основном, а я к нему крайне скептически отношусь в плане игрушек для малышей.
В магазинах полно всего, полки ломятся от товаров, но это все не то. В них нет какой то индивидуальности, да и производство одно китайское в основном, а я к нему крайне скептически отношусь в плане игрушек для малышей.
Поэтому я решила сделать развивающие игрушки из фетра своими руками.
Во первых — фетр экологически чистый и безопасный материал;
Во вторых — идею создания можно подстроить индивидуально под каждого малыша;
Ну и в третьих — конечно же все это делается от сердца с любовью.
Цифры из фетра шаблоны выкройки для вырезания
Для воплощения задумки понадобятся цифры от 1 до 10.
Шаблоны цифр прилагаю. Их можно распечатать, либо через экран монитора перевести на белый лист бумаги или кальки.
Высоту цифр я сделала 3,5 см, однако это зависит от вашей задумки их можно делать и больше и меньше, как необходимо лично вам.
Цифры я перевожу на белый лист жесткого фетра.
Обратите внимание, что цифры я прикладываю наоборот, в зеркальном расположении.
Делаю это для того, чтобы следы от карандаша остались на изнаночной стороне, а не на лицевой.
Как сделать из фетра развивающие игрушки для детей
Помимо цветного фетра понадобятся еще разные пуговки, бусинки, пайетки и другая подходящая фурнитура.
Идея вообще такова: На два квадрата одинакового цвета нужно пришить, на один цифру, на другой квадрат например пуговки (количество пуговок должно соответствовать цифре).
Каждого цвета необходимо нарезать по 4 квадрата, размер квадратов 5*5 см. Фетр должен быть достаточно жесткий, чтобы мог держать форму.
Первым делом пришиваем цифры к одиночным квадратам . Для номера один я взяла салатовый цвет. Цифры стараемся располагать ровно по центру. Шить можно как на швейной машинке, так и вручную. Я шила на машинке, для меня так быстрее.
Далее берем еще один салатовый квадрат и сшиваем их вместе 1-2 мм от края.
На третий салатовый квадрат пришиваем нашу первую пуговку в виде зайчика.
Когда зайка пришит совмещаем заготовку с четвертым квадратом и прошиваем их вместе также по краю на машинке.
У меня есть детали которые не пришиваются их можно только приклеить. Для таких штучек, сначала подготавливаем заготовку, сшивая два квадрата вместе и уже потом клеим мишек и божьих коровок.
Такую фурнитуру я клею на термоклей.
Остальные детали которые не получалось сначала пришить к заготовке, а потом прошивать на машинке (например как бабочки или полосатые бусинки), пришлось пришивать к готовому квадрату и стежки к сожалению остаются на левой стороне и их ни как не спрятать. Но можно минимализировать видимость, например используя не обычные бытовые нитки, а прозрачную мононить. Но зато лицевая сторона получилась очень даже симпатичная, а то что на пару квадратах с обратки видно несколько стежков, по моему это мелочь.
Савелию такие яркие игрушки сразу понравились, он не мог дождаться когда же ему дадут их потрогать. Он очень много раз пытался это сделать, еще в процессе сборки, ведь такие мелкие детали очень привлекательны, особенно его привлекали полосатые бусинки, один раз он даже умудрился их схватить, благо мы вовремя среагировали.
Он очень много раз пытался это сделать, еще в процессе сборки, ведь такие мелкие детали очень привлекательны, особенно его привлекали полосатые бусинки, один раз он даже умудрился их схватить, благо мы вовремя среагировали.
И вот тот момент настал, когда все готово и мелкие детали больше не опасны! Как думаете к чему первому у него потянулась рука?
Правильно — это полосатые бусинки, значит до 10 считать точно научится)
Конечно сейчас он еще совсем маловат, но дети быстро растут и очень быстро все схватывают и если с ними регулярно заниматься, то они способны активно все схватывать и понимать.
Для годовалых малышей пока важно и интересно все потрогать, пощупать и за счет того, что все детали выпуклые и все разной формы и структуры малыши учатся и развивают тактильные ощущения.
Чуть позже малыш благодаря развивающей игре сможет научиться логике и счету. Каждая цифра имеет свой цвет и карточка с таким же цветом имеет такое же количество деталей соответственно цифре.
Развивающие игрушки из фетра для малышей схемы для начинающих
Так же хочется поделиться некоторыми идеями которые мне понравились.
Полезным и развивающим будет сделать ребенку часы. Цифры можно сделать на липучки, чтобы малыш учился сам расставлять их правильно.
шаблон часов со стрелочками.
Еще очень интересной мне показалась тема пазлов из фетра.
Такой вариант тоже помогает учиться считать, запоминать последовательность и мыслить логически.
Такую улитку можно перевести на лист бумаги, а потом вырезать.Детали лучше делать из жесткого фетра или мягкий клеить на картон.
Пазлы могут быть и в другом виде, для малышей помладше такой вариант более подходящий.
Еще для маленьких деток можно сделать разных животных, у которых лапки и хвостик будут съемными на липучках.
Для детей чуть постарше, можно сделать поле из картона и расчертить границы, а из фетра сделать детали как в тетрисе, игра очень увлекательна и развивает логику и мышление, а также пространственное воображение.
Надеюсь что эти идеи вам пригодятся и вы вдохновитесь на создание своим деткам развивающих игрушек.
Рекомендую так же статью по теме Игрушки из фетра своими руками 27 шаблонов с выкройками.
А я на этом с вами прощаюсь, до новых мастер классов!
Объёмные цифры из бумаги своими руками схемы и шаблоны
В последнее время популярностью пользуются большие и маленькие цифры из картона, созданные специально для малышей: их используют для проведения дней рождений и прочих тематических праздников. Мы собрали для вас лучшие варианты объёмных цифр из бумаги своими руками: схемы и шаблоны помогут быстро смастерить нужную комбинацию числового ряда и использовать ее в задуманной идее.
Для чего нужны цифры
Как правило, цифры изготавливаются для праздников. Они необычно смотрятся и вызывают восторг у всех гостей дома: особенно умиляются бабушки и дедушки малыша, ведь цифра не только украшает комнату, но и красноречиво говорит о том, что кроха стал старше. Цифры служат отличным фоном для тематических фотографий: малыш может позировать вместе с многочисленной родней или самостоятельно.
Цифры служат отличным фоном для тематических фотографий: малыш может позировать вместе с многочисленной родней или самостоятельно.
Числовые фигуры делают в любом ивент-агентстве, однако, родители существенно сэкономят, смастерив такие поделки своими руками. Их изготовление необычайно легкое и не занимает много времени: хорошая фантазия и творческие навыки помогут создать цифры из бумаги, которые будут выглядеть не хуже, чем покупные. О том, как это сделать и что для этого нужно подробно расскажем в статье.
Материалы для изготовления
Если в доме совсем маленький малыш, и вы еще не разжились канцелярскими принадлежностями, советуем немедленно отправиться в магазин для рукодельниц. Создайте заметку в телефоне, чтобы не забыть инструменты, которые необходимо приобрести для будущей поделки:
- Картон
Размер картона зависит от размера цифры, которую вы собираетесь смастерить. Для большого количества циферок, планируемых использоваться как реквизит для фотосессии, лучше предпочесть толстый картон А4. если в планах огромные поделки, придется проявить изобретательность и отыскать большие коробки от крупной бытовой техники. Проще всего это сделать, спросив в магазине: обычно продавцы с радостью отдают ненужные упаковки от товара.
Для большого количества циферок, планируемых использоваться как реквизит для фотосессии, лучше предпочесть толстый картон А4. если в планах огромные поделки, придется проявить изобретательность и отыскать большие коробки от крупной бытовой техники. Проще всего это сделать, спросив в магазине: обычно продавцы с радостью отдают ненужные упаковки от товара. - Ножницы
Берите удобные ножницы: при резке картона они не должны тереть места соприкосновения с кожей. - Гофрированная бумага
Если в голове еще нет четкого представления, как должна выглядеть ваша цифра, возьмите цвета, которые наиболее приглянутся в магазине. В противном случае подберите материал согласно задумке. - Бечёвка
Приобретите пару мотков бечёвки, если планируемое мероприятие будет проходить в стиле рустик. - Строительный степлер
Степлер понадобится при работе с плотным картоном. Без него создание объемных фигур станет практически невозможным.
- Клеевой пистолет
Нужен для скрепления деталей - Линейки, карандаши, ластики
Материалы нужны для конструирования и разметки цифр на листах картона. - Дополнительные материалы
Приобретайте дополнительные материалы при необходимости. К ним относятся: текстиль, бусины (бисер), салфетки и цветная бумага, нитки для вязания, мишура.
Делаем каркас объемных цифр
В объемных цифрах есть большое преимущество: ребенок может играть с ними и переставлять в любое место в квартире. При этом качественно сделанная фигура прослужит не один год.
Следуйте инструкции, если хотите смастерить объемную цифру:
- Определитесь с размерами. В зависимости от этого выберите материал: обычный картон размера А4 или большая коробка от холодильника.
- На выбранном куске картона нарисуйте цифру от руки или при помощи шаблона.
 Шаблоны даны ниже.
Шаблоны даны ниже. - Вырежьте цифру. Используйте для этого ножницы или канцелярский нож. Если вы вырежете только одну фигуру, то поделка получится плоской: ее можно повесить на стену или сделать праздничные шпажки с возрастом ребенка.
- Для объемной фигуры подготовьте две одинаковых цифры. Помимо этого, вырежьте полоски из картона, которые послужат прослойкой между шаблонами. Ширину полос определяйте в зависимости от размера цифры.
- Скрепите два шаблона и внутренние полоски при помощи строительного степлера, бумажного скотча или клеевого пистолета.
- Украсьте полученный каркас в зависимости от идеи и материалов, имеющихся в вашем распоряжении.
Варианты объемных цифр из подручных материалов
Мы сделали обширную подборку объемных цифр, созданных мастерицами специально для своих малышей. Некоторые варианты даны с описанием, поэтому у вас не возникнет трудностей с исполнением особенно сложных фигур.
Цифры из бумаги
Великолепные цифры из цветной бумаги делаются очень легко, однако, на их создание нередко уходит несколько дней кропотливой работы. Если вы хотите сделать аккуратную поделку, возьмите создание декоративных элементов в свои руки. Ребенок может оказывать минимальную помощь: подавать листы, выбирать цвета или клеить элементы декора в указанное место. Подробная инструкция для декорирования букв бумажными цветами указана в фотоуроке.
Цифры из пуговиц
Такая цифра выйдет в кругленькую сумму, если вы не являетесь мастерицей, имеющей коллекцию пуговиц. Приклеивайте пуговицы на картон или бумагу, капнув в середину немного суперклея. Если используется тонкий картон и фигура не превышает размера листа А4, пуговицы можно пришить контрастными нитками. Это придаст поделке особенный шарм.
Цифра из фотографий
Цифра с изображениями малыша или семейства исполняется в объемном и плоском варианте. Для закрепления фотографий на бумажной основе нужен клей ПВА или маленькие обрезки скотча.
Для закрепления фотографий на бумажной основе нужен клей ПВА или маленькие обрезки скотча.
Пушистая циферка
Глядя на такие творения трудно сдержать улыбку: они мягкие, пушистые, их хочется трогать. Представьте, как приятно малышу прижиматься к объемной фигурке?
Делать ее легче легкого: подберите нитки для вязания нужных цветов. Дальше следуйте инструкции:
- Намотайте нити на предмет нужно размера. Это может быть обычная кружка или кашпо.
- Аккуратно снимите намотку, сложите ее пополам. Перевяжите сердцевину.
- Разрежьте нитки по краям, распушите. Мягкий помпон готов.
Нитяная поделка
Еще один вариант поделки с использованием нитей для вязания. Просто обмотайте каркас как показано на рисунке. Вы можете оформить композицию единым цветом или смешать несколько контрастов. Для вечеринки в деревенском стиле используйте бечевку.
Цифры из гофрированной бумаги
В этом исполнении фантазии есть где разгуляться. Множество цветов и техник украшения помогут создать фигуру на ваш вкус и под ваши потребности. Здесь и простейшие оборки, и цветы, и обычное оклеивание: смотрите внимательно на фото и черпайте идеи из готовых работ молодых мамочек.
Из салфеток
Не стоит думать, что цифры, сделанные из подручных материалов, будут выглядеть некрасиво, ведь дело мастера боится. Изучите фотографии ниже: все объемные цифры сделаны обычными женщинами. В процессе работы они использовали только шаблоны цифр и салфетки, оказавшиеся дома. Попробуйте и вы: результат превзойдет ожидания!
Из оберточной бумаги
Самый простой вариант, требующий минимум сил и затрат. Приобретите оберточную бумагу, подходящую по стилю к мероприятию, и оберните каркас цифры. Несмотря на простоту, результат получается очень милым. Примеры на фото.
Примеры на фото.
Покупные элементы
Если нет времени вырезать цветы и продумывать детали, приобретите в магазине готовые элементы декора. Это могут быть цветы, бусины или оберточная бумага для цветов.
Ткань
Такой вариант подойдет для любительниц рукоделия. С помощью современных тканей можно создать удивительные рисунки и композиции на цифрах из обычного картона и бумаги.
Делать поделки своими руками несложно. Нужно лишь немного времени, терпения и пара свежих мыслей. Их вы можете почерпнуть из интернета, в том числе и из статьи «Объёмные цифры из бумаги своими руками: схемы и шаблоны».
Распечатать цифру 1 | Распечатать цифру 2 | Распечатать цифру 3 | Распечатать цифру 4 |
Распечатать цифру 5 | Распечатать цифру 6 | Распечатать цифру 7 | Распечатать цифру 8 |
Распечатать цифру 9 | Распечатать цифру 10 | Распечатать цифру 11 | Распечатать цифру 12 |
Распечатать цифру 13 | Распечатать цифру 14 | Распечатать цифру 15 | Распечатать цифру 16 |
Распечатать цифру 17 | Распечатать цифру 18 | Распечатать цифру 19 | Распечатать цифру 20 |
Распечатать цифру 21 | Распечатать цифру 22 | Распечатать цифру 23 | Распечатать цифру 24 |
Распечатать цифру 25 | Распечатать цифру 26 | Распечатать цифру 27 | Распечатать цифру 28 |
Распечатать цифру 29 | Распечатать цифру 30 | Распечатать цифру 31 | Распечатать цифру 32 |
Распечатать цифру 33 | Распечатать цифру 34 | Распечатать цифру 35 | Распечатать цифру 36 |
Распечатать цифру 37 | Распечатать цифру 38 | Распечатать цифру 39 | Распечатать цифру 40 |
Распечатать цифру 41 | Распечатать цифру 42 | Распечатать цифру 43 | Распечатать цифру 44 |
Распечатать цифру 45 | Распечатать цифру 46 | Распечатать цифру 47 | Распечатать цифру 48 |
Распечатать цифру 49 | Распечатать цифру 50 | Распечатать цифру 51 | Распечатать цифру 52 |
Распечатать цифру 53 | Распечатать цифру 54 | Распечатать цифру 55 | Распечатать цифру 56 |
Распечатать цифру 57 | Распечатать цифру 58 | Распечатать цифру 59 | Распечатать цифру 60 |
Распечатать цифру 61 | Распечатать цифру 62 | Распечатать цифру 63 | Распечатать цифру 64 |
Распечатать цифру 65 | Распечатать цифру 66 | Распечатать цифру 67 | Распечатать цифру 68 |
Распечатать цифру 69 | Распечатать цифру 70 | Распечатать цифру 71 | Распечатать цифру 72 |
Распечатать цифру 73 | Распечатать цифру 74 | Распечатать цифру 75 | Распечатать цифру 76 |
Распечатать цифру 77 | Распечатать цифру 78 | Распечатать цифру 79 | Распечатать цифру 80 |
Распечатать цифру 81 | Распечатать цифру 82 | Распечатать цифру 83 | Распечатать цифру 84 |
Распечатать цифру 85 | Распечатать цифру 86 | Распечатать цифру 87 | Распечатать цифру 88 |
Распечатать цифру 89 | Распечатать цифру 90 | Распечатать цифру 91 | Распечатать цифру 92 |
Распечатать цифру 93 | Распечатать цифру 94 | Распечатать цифру 95 | Распечатать цифру 96 |
Распечатать цифру 97 | Распечатать цифру 98 | Распечатать цифру 99 |
Шаблоны чисел
Эта страница содержит ссылки на бесплатные рабочие листы по математике для задач шаблонов чисел.:max_bytes(150000):strip_icc()/NUMBERS-08-56a80f0e5f9b58b7d0f045eb.png) Нажмите одну из кнопок ниже, чтобы увидеть все рабочие листы в каждом наборе. Вы также можете использовать меню «Рабочие листы» сбоку на этой странице, чтобы найти рабочие листы по другим математическим темам.
Нажмите одну из кнопок ниже, чтобы увидеть все рабочие листы в каждом наборе. Вы также можете использовать меню «Рабочие листы» сбоку на этой странице, чтобы найти рабочие листы по другим математическим темам.
Рабочие листы с образцами чисел
Рабочие листы с образцами чисел на этой странице – отличная практика для тестов по математике, с которыми ваши ученики будут сталкиваться в классе или при проверке состояния. В то время как числовые шаблоны часто упоминаются лишь кратко во многих учебных программах по математике, практика с числовыми шаблонами – отличный способ повысить не только результаты тестов, но и беглость числовых навыков.
Что такое числовые шаблоны?
Числовые шаблоны – очень распространенный тип задач, когда студенту дается последовательность чисел и просят определить, как этот список создается и какими будут следующие значения. Это обычные функции стандартизированных тестов, и вы также найдете их как часть стандарта Common Core (в частности, 4.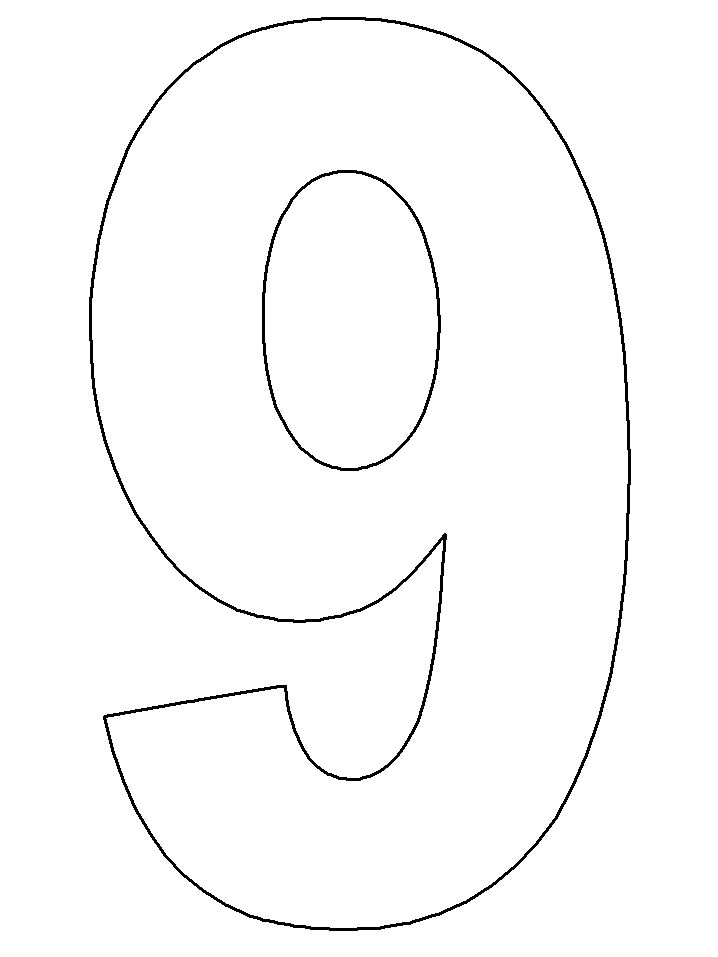 0A.C.5) в Соединенных Штатах. Простые числовые шаблоны обычно вводятся в 4-м классе, а их концепции усиливаются в 5-м и 6-м классах, но более сложные геометрические числовые шаблоны с более сложными правилами (например, последовательность Фибоначчи) являются распространенными вопросами теста на протяжении всех классов средней школы.
0A.C.5) в Соединенных Штатах. Простые числовые шаблоны обычно вводятся в 4-м классе, а их концепции усиливаются в 5-м и 6-м классах, но более сложные геометрические числовые шаблоны с более сложными правилами (например, последовательность Фибоначчи) являются распространенными вопросами теста на протяжении всех классов средней школы.
Обучение студентов распознаванию и пониманию числовых образов выходит за рамки фундаментальных арифметических навыков и также обучает логике и навыкам распознавания образов. В типичной задаче о числовом шаблоне ученику дается последовательность чисел, а затем он должен описать правило или шаблон, генерирующий числа. Часто задача требует, чтобы учащийся указал следующие числа в шаблоне, но некоторые варианты задачи также будут запрашивать предыдущие числа. Требование от ученика проработать шаблон вперед и назад – один из способов обеспечить полное понимание.
Базовые шаблоны чисел
Самые основные типы шаблонов чисел включают в себя базовые правила сложения и вычитания, и они используют знакомство учащихся с шаблонами подсчета пропусков для быстрого создания соответствующего правила.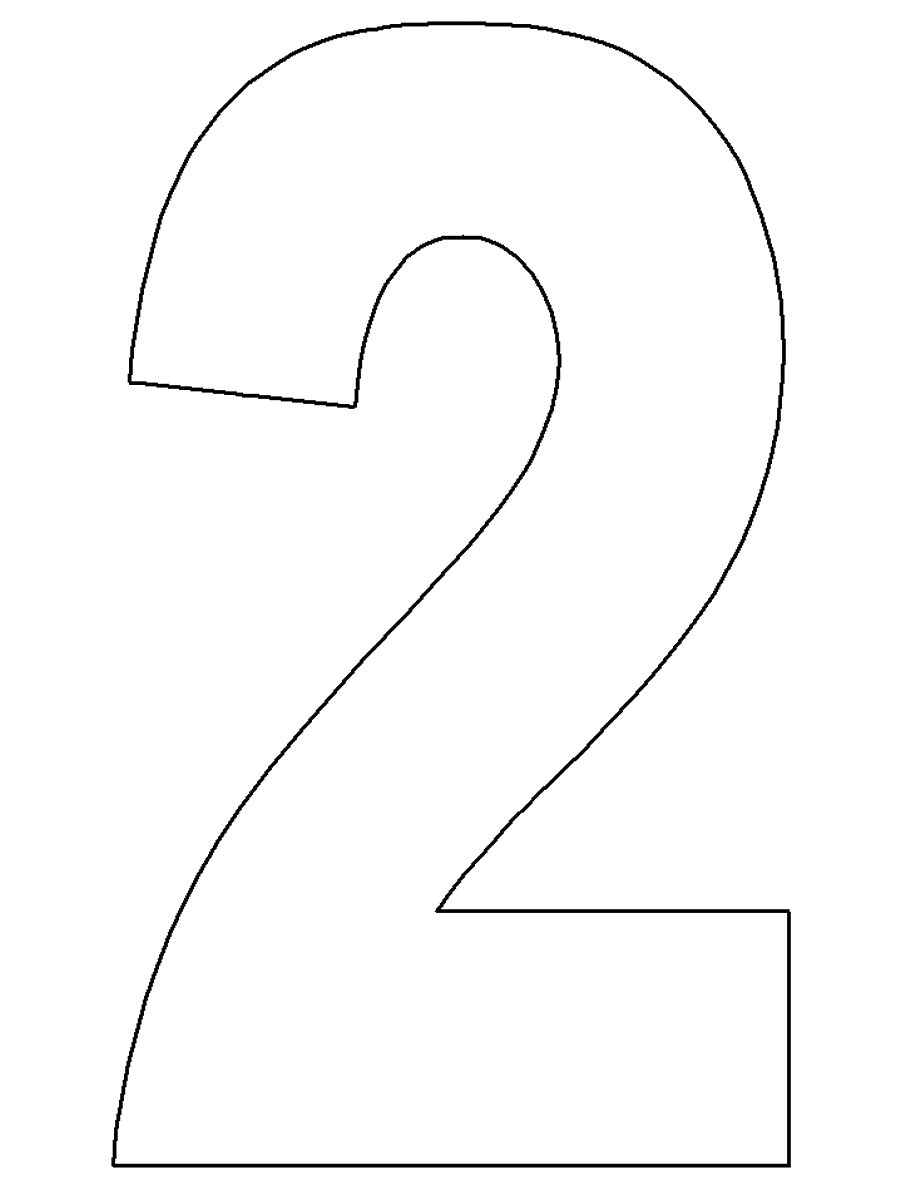 Многие из этих числовых шаблонов будут начинаться с числа, расположенного выше в последовательности (например, если шаблон – «добавить 3», обеспечивая последовательность «12, 15, 18 …»).
Многие из этих числовых шаблонов будут начинаться с числа, расположенного выше в последовательности (например, если шаблон – «добавить 3», обеспечивая последовательность «12, 15, 18 …»).
Варианты с обратным отсчетом паттернов (например, паттерн «минус 3» с последовательностью «21, 18, 15… “) вводят шаблоны чисел вычитания.
Шаблоны чисел также являются отличным способом постепенного повышения уверенности в распознавании последовательностей в незнакомом контексте. Например, шаблон подсчета по тройкам, описанный выше, может начинаться с числа, которое обычно не входит в знакомый шаблон. (например, «5, 8, 11 …»), что дает возможность изучающему математику заново открыть для себя знакомый числовой шаблон.
Числовые шаблоны с обычными приращениями
Многие из рабочих листов числовых шаблонов на этом page имеют дело с приращениями, которые часто встречаются в реальных последовательностях чисел, и способность быстро идентифицировать эти закономерности является полезным навыком. Здесь вы найдете образцы пятерок, образцы десятков, образцы пятнадцати и образцы 25 для практики. Это также отличная практика, когда учащиеся овладевают базовыми шаблонами сложения чисел или шаблонов чисел вычитания, когда они ищут что-то немного более сложное.
Здесь вы найдете образцы пятерок, образцы десятков, образцы пятнадцати и образцы 25 для практики. Это также отличная практика, когда учащиеся овладевают базовыми шаблонами сложения чисел или шаблонов чисел вычитания, когда они ищут что-то немного более сложное.
Шаблоны чисел умножения и не только
На этой странице также есть набор рабочих листов, в которых есть правила шаблонов, использующие операции умножения и деления. Хотя этот тип числового шаблона менее распространен в 4-м или 5-м классе, когда умножение только вводится, вы довольно часто встретите шаблоны умножения чисел на вступительных экзаменах в колледж, поэтому важно знакомство с этими шаблонами.
Шаблоны чисел умножения служат мостом к шаблонам геометрических чисел, таким как последовательность Фибоначчи. Это шаблоны, в которых следующая последовательность значений зависит от предыдущих чисел. Паттерн Фибоначчи включает суммирование двух предшествующих цифр в последовательности, поэтому правило, по сути, «сложите два предыдущих числа». Канонический паттерн Фибоначчи – «0, 1, 1, 2, 3, 5, 8 …» и аналогичный, но вы часто будете видеть проблемы с числовым паттерном, которые начинаются с другой базы и используют то же правило.
Канонический паттерн Фибоначчи – «0, 1, 1, 2, 3, 5, 8 …» и аналогичный, но вы часто будете видеть проблемы с числовым паттерном, которые начинаются с другой базы и используют то же правило.
Другие шаблоны чисел
Другие типы шаблонов чисел, которые могут возникать, представляют собой просто списки общих чисел, например, шансы или равенства, простые числа, составные числа, времена. Усиление концепции шаблонов, встречающихся практически в любом приложении, позволит студентам определить их, когда они появляются как в математических тестах, так и в реальной жизни.
Шаблоны чисел
Последовательность – это шаблон чисел, которые формируются в соответствии с
определенное правило.
Мы часто можем описать числовые шаблоны более чем одним способом. К
Чтобы проиллюстрировать это, рассмотрим следующую последовательность чисел {1, 3, 5, 7, 9,
}.
Очевидно, что первый член этого числового шаблона равен 1; и условия после
первый член получается добавлением 2 к предыдущему члену. Мы можем
Мы можем
также опишите этот шаблон чисел как набор нечетных чисел.
Методом проб и ошибок находим:
Наблюдая, мы замечаем, что мы можем описать этот числовой паттерн с помощью
Правило
Формулы и таблицы
Таблицу значений можно сгенерировать из правила
, как показано ниже.
Нахождение алгебраического правила
Мы используем алгебру для изучения правил, описывающих поведение повседневных
вещи. Например, поведение высоты мяча, когда он
выброшены вверх или сумма непогашенной ссуды после ряда регулярных
выплаты. Найдя закономерность в наблюдаемых значениях (т. Е.
Е.
измерений), мы часто можем обнаружить правило, которое позволяет нам
точные прогнозы.
Использование разностного шаблона
Когда мы пытаемся найти алгебраическое правило для упорядоченного
пары, мы можем найти
разница между двумя последовательными значениями y . Это позволяет
нам найти правило, как показано ниже.
Рассмотрим следующую таблицу.
Мы замечаем, что значения x увеличиваются только по одному за раз и
разница между последовательными значениями и равна 2.Итак, правило
начинается с y = 2 x . Это даст правильный ответ от
стол? Давайте проверим.
Ответ – нет. Из таблицы, когда x = 1,
значение y должно быть 5. Как нам изменить наш ответ с 2 на 5?
Как нам изменить наш ответ с 2 на 5?
Мы
следует добавить 3.
Проверьте правило, чтобы убедиться в его правильности:
Пример 5
Найдите правило для следующей таблицы значений:
Решение:
В данной таблице значения x увеличиваются на 1 для каждого заказанного
пара.
Найдите разницу между последовательными значениями и . То есть:
Разница между последовательными значениями и всегда равна 3. Итак,
Правило имеет вид
Чек:
Проверьте правило, чтобы убедиться в его правильности:
Итак, наше правило верно.
Примечание:
Чтобы установить правило для числового шаблона, включающего упорядоченные
пары x и y , мы можем
найти разницу между каждыми двумя последовательными значениями y . Если
шаблон разности такой же, то коэффициент x в алгебраическом правиле (или формуле) совпадает с шаблоном разности.
Ключевые термины
числовой образец, последовательность, алгебраический
правило, разностный паттерн
Типы числовых паттернов в математике
Изучая математические паттерны, люди узнают о закономерностях в нашем мире.Наблюдение за образцами позволяет людям развивать свою способность предсказывать будущее поведение природных организмов и явлений. Инженеры-строители могут использовать свои наблюдения за схемами движения для строительства более безопасных городов. Метеорологи используют шаблоны для предсказания гроз, торнадо и ураганов. Сейсмологи используют шаблоны для прогнозирования землетрясений и оползней. Математические модели полезны во всех областях науки.
Сейсмологи используют шаблоны для прогнозирования землетрясений и оползней. Математические модели полезны во всех областях науки.
Арифметическая последовательность
Последовательность – это группа чисел, которые следуют шаблону на основе определенного правила.Арифметическая последовательность включает в себя последовательность чисел, к которой добавлено или вычтено одинаковое количество. Сумма, которая добавляется или вычитается, называется общей разницей. Например, в последовательности «1, 4, 7, 10, 13…» каждое число было добавлено к 3, чтобы получить последующее число. Общее различие для этой последовательности – 3.
Геометрическая последовательность
Геометрическая последовательность – это список чисел, которые умножаются (или делятся) на одинаковую величину. Величина, на которую умножаются числа, называется обычным соотношением.Например, в последовательности «2, 4, 8, 16, 32 …» каждое число умножается на 2. Число 2 является обычным соотношением для этой геометрической последовательности.
Число 2 является обычным соотношением для этой геометрической последовательности.
Треугольные числа
Числа в последовательности называются терминами. Члены треугольной последовательности связаны с количеством точек, необходимых для создания треугольника. Вы начнете формировать треугольник из трех точек; один сверху и два снизу. В следующем ряду будет три точки, всего шесть точек. В следующем ряду треугольника будет четыре точки, а всего будет 10 точек.В следующем ряду будет пять точек, всего 15 точек. Следовательно, треугольная последовательность начинается: «1, 3, 6, 10, 15…»)
Квадратные числа
В последовательности квадратных чисел члены являются квадратами их положения в последовательности. Последовательность квадратов начинается с «1, 4, 9, 16, 25…»
Числа куба
В последовательности чисел куба элементы – это кубы, соответствующие их положению в последовательности. Следовательно, последовательность куба начинается с «1, 8, 27, 64, 125…»
Следовательно, последовательность куба начинается с «1, 8, 27, 64, 125…»
Числа Фибоначчи
В числовой последовательности Фибоначчи члены находятся путем сложения двух предыдущих членов.Последовательность Фибоначчи начинается таким образом: «0, 1, 1, 2, 3, 5, 8, 13…» Последовательность Фибоначчи названа в честь Леонардо Фибоначчи, родившегося в 1170 году в Пизе, Италия. Фибоначчи познакомил европейцев с индо-арабскими цифрами с публикацией своей книги «Liber Abaci» в 1202 году. Он также представил последовательность Фибоначчи, которая уже была известна индийским математикам. Последовательность важна, потому что она появляется во многих местах в природе, в том числе: узоры листьев растений, узоры спиральных галактик и измерения наутилуса в камерах.
Рабочие листы с образцами номеров | Что такое, как определить, важность
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатный образец. Загрузить образец
Загрузить этот образец
Этот образец предназначен исключительно для участников KidsKonnect!
Чтобы загрузить этот рабочий лист, нажмите кнопку ниже, чтобы зарегистрироваться бесплатно (это займет всего минуту), и вы вернетесь обратно на эту страницу, чтобы начать загрузку!
Зарегистрируйтесь
Уже зарегистрировались? Авторизуйтесь, чтобы скачать.
Когда нам дается группа чисел и мы наблюдаем, что они следуют последовательности, такие группы включают шаблонов номеров . Эти шаблоны помогают нам лучше визуализировать и понимать числа.
См. Файл фактов ниже для получения дополнительной информации о шаблоне чисел или, в качестве альтернативы, вы можете загрузить нашу 28-страничную рабочую таблицу шаблонов номеров, чтобы использовать их в классе или дома. Этот рабочий лист разбит на начальный, средний и продвинутый, что означает, что вы можете выбрать уровень сложности для своего ученика.
Основные факты и информация
Резюме:
- Группы чисел часто следуют последовательности или шаблону.
- Выявление таких закономерностей помогает нам предсказывать решения.
- Помогает определить связь между числами.
Что такое числовой шаблон?
- Когда нам дается группа чисел и мы наблюдаем, что они следуют последовательности, такие группы включают образцы чисел.

- Эти шаблоны помогают нам лучше визуализировать и понимать числа.
- Эта концепция также является одним из основных строительных блоков при изучении математики.
- Если вы можете найти шаблон, то решение легко найти.
- Предположим, у нас есть группа чисел:
- Наблюдая за этими числами, мы обнаруживаем, что начальное число равно 1, и добавляя два, мы получаем следующее число. Это также можно увидеть в числовой строке:
- Следовательно, мы можем сказать, что здесь соблюдается определенный шаблон.
Как определить эти закономерности?
- Когда мы начинаем работать с числовыми группами, мы начинаем замечать, что большинство из них имеют шаблон или последовательность.
- Выявление этих закономерностей важно, и это приходит с практикой.
- Чем больше вы практикуетесь с числами, тем легче определить скрытый шаблон, по которому они следуют. Как только мы узнаем, как идентифицировать эти закономерности, вычисления станут проще.

- Напомним:
- Подсчет пропусков также следует определенному шаблону чисел.Когда пропускаем счет на 2, мы прыгаем с интервалом в два. Точно так же, когда мы пропускаем счет на 3, 4 и 5 секунд, мы перескакиваем на интервалы 3, 4 и 5. Следовательно, мы также можем определить закономерность при подсчете пропусков.
Важность числовых паттернов
- Изучение числовых паттернов помогает заложить прочный фундамент в математике и поможет в работе с числами.
- Дети смогут узнать отношения, существующие между числами.
- Дети научатся наблюдать за последовательностями и смогут предсказывать, что будет дальше.Этот навык пригодится им на протяжении всего курса.
- Эти шаблоны помогают учащимся понять умножение и сложение.
Пример № 1:
- Мы начнем с некоторых основных примеров, которые помогут нам определить и предсказать недостающие числа.
- См. Группу номеров, приведенную ниже:
2, 4, 6, 8, 10,?
- Наблюдая за этой группой, мы понимаем, что, начиная с нуля, мы получаем следующее число, перепрыгивая на две единицы.

- Это также пример подсчета пропусков на 2, начиная с нуля. Это также напоминает таблицу умножения двух.
- Итак, мы можем сказать, что все эти концепции взаимосвязаны друг с другом. Поняв одну концепцию, мы можем получить полное представление обо всех связанных концепциях.
- Мы будем использовать числовую строку, чтобы получить ответ.
- Следовательно, перескочив на две единицы вправо, начиная с 10, мы получим ответ 12. Итак, 12 – это отсутствующее число.
Пример № 2:
- Теперь у нас есть другая последовательность:
0, 4, 8,?
- Это снова похоже на подсчет пропусков на 4, начиная с нуля, и таблицу умножения на 4.
- Мы снова будем использовать числовую строку два, чтобы определить шаблон и найти недостающее число.
- Стоя на 8, мы прыгаем на 4 юнита вправо и приземляемся на 12, которое является недостающим числом.
Пример № 3:
- Теперь мы решаем пример числа, которое не начинается с нуля и имеет несколько пропущенных чисел между ними.

- Рассмотрим следующую последовательность:
6, 9, 12, 15,?, 21, 24,?, 30, 33
- Наблюдая за вышеуказанными числами, мы замечаем, что добавляется число 3 чтобы получить следующее число
- Следовательно, добавляя 3 к 15, мы получаем недостающее число 18, а добавляя 3 к 24, мы получаем недостающее число 27.
Пример № 4:
- Рассмотрим числовую последовательность, приведенную ниже :
17, 19, 21,?, 25,?, 29
- Когда мы наблюдаем первое и второе числа, мы видим, что они разделены интервалом 2.
- Мы наблюдаем ту же закономерность во втором и третьем числе.
- Следовательно, добавляя 2 к 21, мы получаем 23, которое является первым отсутствующим числом, а добавляя 2 к 25, мы получаем 27, которое является вторым отсутствующим числом.
Пример № 5:
- Есть также группа чисел, где числа уменьшаются в значении по определенному шаблону.

- Этот шаблон необходимо идентифицировать, чтобы найти недостающие числа.
- Это похоже на приведенные выше примеры, но в этом случае вместо добавления числа к предыдущему числу, чтобы получить следующее число, мы вычитаем определенное число, чтобы получить следующее число.
- Дан простой пример для понимания концепции. Рассмотрим следующую группу чисел:
20, 15, 10,?, 0
- Когда мы наблюдаем, мы идентифицируем, что числа вычитаются на 5, чтобы получить следующее число.
- Другими словами, мы также можем сказать, что мы перемещаем 5 единиц влево от числовой строки, чтобы получить следующее число.
- Следовательно, в приведенном выше примере отсутствует номер 5.
Листы шаблонов номеров
Это фантастический комплект, который включает в себя все, что вам нужно знать о шаблонах номеров на 28 страницах с подробным описанием.Это готовых к использованию листов с образцами чисел, которые идеально подходят для обучения учащихся работе с образцами чисел. Когда нам дается группа чисел и мы наблюдаем, что они следуют последовательности, такие группы включают образцы чисел. Эти шаблоны помогают нам лучше визуализировать и понимать числа.
Когда нам дается группа чисел и мы наблюдаем, что они следуют последовательности, такие группы включают образцы чисел. Эти шаблоны помогают нам лучше визуализировать и понимать числа.
Полный список включенных рабочих листов
- Рабочий лист 1 (новичок)
- Рабочий лист 2 (новичок)
- Рабочий лист 3 (новичок)
- Рабочий лист 4 (начинающий
- Рабочий лист 5 (промежуточный) )
- Рабочий лист 7 (средний уровень)
- Рабочий лист 8 (средний уровень)
- Рабочий лист 9 (предварительный)
- Рабочий лист 10 (предварительный)
- Рабочий лист 11 (предварительный)
- Рабочий лист 12 (предварительный)
Ссылка / цитируйте это страница
Если вы ссылаетесь на какой-либо контент на этой странице на своем собственном веб-сайте, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник.
Таблицы шаблонов номеров: https://kidskonnect. com – KidsKonnect, 6 марта 2019 г. Появится ссылка
com – KidsKonnect, 6 марта 2019 г. Появится ссылка
как листы шаблонов номеров: https://kidskonnect.com – KidsKonnect, 6 марта 2019 г.
Использование с любой учебной программой
Эти рабочие листы были специально разработаны для использования с любой международной учебной программой. Вы можете использовать эти рабочие листы как есть или редактировать их с помощью Google Slides, чтобы сделать их более конкретными в соответствии с вашими уровнями способностей учащихся и стандартами учебной программы.
Описание последовательностей | Числовые шаблоны
3.2 Описание последовательностей (EMAY)
Последовательность – это упорядоченный список элементов, обычно чисел. Каждый элемент, составляющий последовательность, называется «термином».
Последовательности могут иметь интересные паттерны. Здесь мы исследуем некоторые типы паттернов и то, как они формируются.
Примеры:
\ (1; 4; 7; 10; 13; 16; 19; 22; 25; \ ldots \)
Между последовательными терминами есть разница в \ (\ text {3} \).

Шаблон продолжается добавлением \ (\ text {3} \) к предыдущему члену.
\ (13; 8; 3; -2; -7; -12; -17; -22; \ ldots \)
Между последовательными терминами существует разница в \ (- \ text {5} \).
Шаблон продолжается добавлением \ (- \ text {5} \) к предыдущему члену (т. Е. Вычитанием \ (\ text {5} \) из).
\ (2; 4; 8; 16; 32; 64; 128; 256; \ ldots \)
Эта последовательность имеет множитель \ (\ text {2} \) между последовательными членами.
Модель продолжается путем умножения предыдущего члена на 2.
\ (3; -9; 27; -81; 243; -729; 2187; \ ldots \)
Эта последовательность имеет множитель \ (- \ text {3} \) между последовательными членами.
Шаблон продолжается путем умножения предыдущего члена на \ (- \ text {3} \).
\ (9; 3; 1; \ frac {1} {3}; \ frac {1} {9}; \ frac {1} {27}; \ ldots \)
Эта последовательность имеет коэффициент \ (\ frac {1} {3} \) между последовательными членами.
 {3}; \ ldots \) и посмотрите узор с полномочиями. Вы можете обсудить это в классе как предшественник геометрических рядов, которые будут представлены в 12 классе.
{3}; \ ldots \) и посмотрите узор с полномочиями. Вы можете обсудить это в классе как предшественник геометрических рядов, которые будут представлены в 12 классе.Рабочий пример 1: Учебный стол
Вы и \ (\ text {3} \) друзья решили изучать математику и сидите вместе за квадратным столом. Через несколько минут приходят \ (\ text {2} \) другие друзья и хотят сесть за ваш столик. Вы перемещаете другой стол рядом со своим, чтобы \ (\ text {6} \) люди могли сесть за стол.Другие \ (\ text {2} \) друзья также хотят присоединиться к вашей группе, поэтому вы берете третью таблицу и добавляете ее к существующим таблицам. Теперь \ (\ text {8} \) люди могут сидеть вместе.
Изучите, как количество сидящих людей связано с количеством столов. Есть закономерность?
Рисунок 3.1: За каждым добавленным столом могут сесть еще два человека.
Составьте таблицу, чтобы увидеть, образуется ли узор
Количество столиков , n
Количество сидящих людей
\ (\ text {1} \)
\ (4 = 4 \)
\ (\ text {2} \)
\ (4 + 2 = 6 \)
\ (\ text {3} \)
\ (4 + 2 + 2 = 8 \)
\ (\ text {4} \)
\ (4 + 2 + 2 + 2 = 10 \)
\ (\ vdots \)
\ (\ vdots \)
n
\ (4 + 2 + 2 + 2 + \ cdots +2 \)
Опишите узор
Мы видим, что для \ (\ text {3} \) столов мы можем разместить \ (\ text {8} \) людей, для \ (\ text {4} \) столов мы можем разместить \ (\ text {10 } \) люди и так далее.
 {\ text {th}} \) и записывается как \ ({T} _ {n} \).{\ text {th}} \) член определяется общей формулой:
{\ text {th}} \) и записывается как \ ({T} _ {n} \).{\ text {th}} \) член определяется общей формулой:\ ({T} _ {n} = 2n-1 \)
Вы можете проверить это, подставив значения в формулу:
\ begin {align *}
{T} _ {1} & = 2 \ left (1 \ right) -1 = 1 \\
{T} _ {2} & = 2 \ left (2 \ right) -1 = 3 \\
{T} _ {3} & = 2 \ left (3 \ right) -1 = 5 \\
{T} _ {4} & = 2 \ left (4 \ right) -1 = 7 \\
{T} _ {5} & = 2 \ left (5 \ right) -1 = 9
\ end {выровнять *}Если мы найдем взаимосвязь между положением термина и его значением, мы сможем найти общую формулу, которая соответствует шаблону, и найти любой термин в последовательности.{\ text {th}} \) срок? Попробуем сделать это с помощью таблицы.
Номер срока \ (T_ {1} \)
\ (T_ {2} \)
\ (T_ {3} \)
\ (T_ { 4} \)
\ ({T} _ {n} \)
Срок \ (\ text {6} \)
\ (\ text {1} \)
\ (- \ text {4} \)
\ (- \ text {9} \)
\ ({T} _ {n} \)
Формула \ (6-0 \ раз 5 \)
\ (6-1 \ раз 5 \)
\ (6-2 \ раз 5 \)
\ ( 6-3 \ умножить на 5 \)
\ (6 – (n-1) \ умножить на 5 \)
Вы можете видеть, что разница между последовательными членами всегда является коэффициентом при \ (n \ ) в формуле.
 Это называется общей разницей .
Это называется общей разницей .Следовательно, для последовательностей с общей разницей общая формула всегда будет иметь вид: \ (T_ {n} = dn + c \), где \ (d \) – разница между каждым членом и \ (c \) некоторая константа.
Последовательности с общим отличием называются линейными последовательностями.
- Общая разница
Общее различие – это разница между любым термином и термином перед ним. Общее различие обозначается \ (d \).
Например, рассмотрим последовательность \ (10; 7; 4; 1; \ ldots \)
Чтобы вычислить общую разницу, мы находим разницу между любым термином и предыдущим термином.
Найдем общую разницу между первыми двумя терминами.
\ begin {align *}
d & = {T} _ {2} – {T} _ {1} \\
& = 7-10 \\
& = -3
\ end {выровнять *}Проверим еще два термина:
\ begin {align *}
d & = {T} _ {4} – {T} _ {3} \\
& = 1-4 \\
& = -3
\ end {выровнять *}Мы видим, что \ (d \) постоянно.

В общем, \ (d = T_ {n} -T_ {n-1} \)
\ (d \ ne T_ {n-1} -T_ {n} \) например, \ (d = {T} _ {2} – {T} _ {1} \), а не \ ({T} _ {1} – {T} _ {2} \).
Рабочий пример 2: Учебный стол, продолжение
Как и раньше, вы и \ (\ text {3} \) друзья изучаете математику и сидите вместе за квадратным столом. Через несколько минут \ (\ text {2} \) приходят другие друзья, поэтому вы перемещаете другой столик рядом со своим. Теперь \ (\ text {6} \) люди могут сидеть за столом. К вашей группе также присоединяются другие \ (\ text {2} \) друзья, поэтому вы берете третью таблицу и добавляете ее к существующим.Теперь \ (\ text {8} \) люди могут сидеть вместе, как показано ниже.
Найдите выражение для количества людей, сидящих за \ (n \) столами.
Используйте общую формулу, чтобы определить, сколько человек может сидеть за \ (\ text {12} \) столами.
Сколько столов нужно, чтобы разместить \ (\ text {20} \) человек?
Рисунок 3.2: За каждым добавленным столом могут сесть еще два человека.
Составьте таблицу, чтобы увидеть выкройку
Количество столов , \ (n \)
Количество сидящих людей
Образец
\ (\ text {1}) \ (\ text {1})
\ (4 = 4 \)
\ (= 4 + 2 \ left (0 \ right) \)
\ (\ text {2} \)
\ (4+ 2 = 6 \)
\ (= 4 + 2 \ left (1 \ right) \)
\ (\ text {3} \)
\ (4 + 2 + 2 = 8 \)
\ (= 4 + 2 \ left (2 \ right) \)
\ (\ text {4} \)
\ (4 + 2 + 2 + 2 = 10 \)
\ (= 4 + 2 \ left (3 \ right) \)
\ (\ vdots \)
\ (\ vdots \)
\ (\ vdots \)
n
\ (4 + 2 + 2 + 2 + \ cdots +2 \)
\ (= 4+ 2 \ left (n-1 \ right) \)
Примечание: Вы можете по-разному относиться к шаблону в этой задаче.{\ text {th}} \) термин, другими словами, найти \ ({T} _ {n} \), если \ (n = 12 \)
\ begin {align *}
{T} _ {12} & = 4 + 2 \ влево (12-1 \ вправо) \\
& = 4 + 2 \ влево (11 \ вправо) \\
& = 4 + 22 \\
& = 26
\ end {выровнять *}Следовательно, \ (\ text {26} \) люди могут сидеть за \ (\ text {12} \) столами.
Рассчитайте количество столов, необходимых для размещения \ (\ text {20} \) людей, другими словами, найдите \ (n \), если \ ({T} _ {n} = 20 \)
\ begin {align *}
{T} _ {n} & = 4 + 2 \ left (n-1 \ right) \\
20 & = 4 + 2 \ влево (п-1 \ вправо) \\
20 & = 4 + 2н-2 \\
20-4 + 2 & = 2n \\
18 & = 2n \\
\ frac {18} {2} & = n \\
n & = 9
\ end {выровнять *}Следовательно, \ (\ text {9} \) столы необходимы для размещения \ (\ text {20} \) людей.
Важно отметить разницу между \ (n \) и \ ({T} _ {n} \). \ (n \) можно сравнить с заполнителем, указывающим позицию термина в последовательности, а \ ({T} _ {n} \) – это значение места, занимаемого \ (n \). В нашем примере выше первая таблица содержит \ (\ text {4} \) людей. Итак, для \ (n = 1 \) значение \ ({T} _ {1} = 4 \) и так далее:
\ (n \)
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
\ (\ ldots \)
\ ({T} _ {n} \)
\ (\ text {4} \ )
\ (\ text {6} \)
\ (\ text {8} \)
\ (\ text {10} \)
\ (\ ldots \)
Рабочий пример 3: тарифные планы
Raymond подписывается на тарифный план с ограниченным доступом от Vodacell.Тарифные планы с ограниченным трафиком стоят \ (\ text {R} \, \ text {120} \) за \ (\ text {1} \) гигабайт (ГБ) в месяц, \ (\ text {R} \, \ text { 135} \) для \ (\ text {2} \) \ (\ text {GB} \) в месяц и \ (\ text {R} \, \ text {150} \) для \ (\ text {3} \) \ (\ text {GB} \) в месяц. Предположим, этот образец продолжается бесконечно.
Используйте таблицу для настройки структуры стоимости тарифных планов.
Найдите общую формулу последовательности.
Используйте общую формулу для определения стоимости тарифного плана \ (\ text {30} \) \ (\ text {GB} \).
- Стоимость безлимитного тарифного плана составляет \ (\ text {R} \, \ text {520} \) в месяц. Определите объем данных, которые Раймонд должен будет использовать, чтобы ему было дешевле подписаться на безлимитный план.
Составьте таблицу, чтобы увидеть выкройку
Номер ГБ \ ((n) \)
\ (\ text {1} \)
\ (\ text {2} \)
\ (\ text {3} \)
\ (\ text {4} \)
Стоимость (в рэндах)
\ (\ text {120} \)
\ ( \ text {135} \)
\ (\ text {150} \)
\ (\ text {165} \)
Pattern
\ (\ text {120} \)
\ (120+ (1) (15) = 135 \)
\ (120+ (2) (15) = 150 \)
\ (120+ ( 3) (15) = 165 \)
Используйте наблюдаемую закономерность, чтобы определить общую формулу.{\ text {th}} \), другими словами, найти \ ({T} _ {n} \), если \ (n = 30 \). Используя общую формулу, получаем:
\ begin {align *}
{T} _ {n} & = 120 + 15 \ влево (n-1 \ вправо) \\
\ поэтому {T} _ {30} & = 120 + 15 \ left (30-1 \ right) \\
& = 120 + 15 \ влево (29 \ вправо) \\
& = 120 + 435 \\
& = 555
\ end {выровнять *}Следовательно, стоимость пакета данных \ (\ text {30} \) \ (\ text {GB} \) составляет \ (\ text {R} \, \ text {555} \).
Определите, когда будет дешевле приобрести безлимитный тарифный план
Последний вопрос этого рабочего примера требует от нас определить, когда для Раймонда будет дешевле приобрести безлимитный тарифный план вместо ограниченного.Другими словами, нам нужно найти \ (n \), где \ (T_n \) меньше, чем \ (\ text {R} \, \ text {520} \).
Мы знаем, что:
\ [{T} _ {n} = 120 + 15 \ влево (n-1 \ вправо) \]
Следовательно, если \ (T_n = 520 = 120 + 15 \ left (n-1 \ right) \)
Решая для \ (n \), получаем:
\ begin {align *}
520 & = 120 + 15 \ влево (п-1 \ вправо) \\
520 & = 120 + 15н-15 \\
520 & = 105 + 15n \\
405 & = 15n \\
\ frac {405} {15} & = n \\
n & = 27
\ end {выровнять *}Следовательно, для Раймонда дешевле приобрести безлимитный тарифный план, если он использует более \ (\ text {27} \) \ (\ text {GB} \) в месяц.
Siyavula Practice дает вам доступ к неограниченному количеству вопросов с ответами, которые помогут вам в обучении. Тренируйтесь где угодно, когда угодно и на любом устройстве!
Зарегистрируйтесь, чтобы попрактиковаться
Упражнение 3.1
Используйте данный образец для заполнения таблицы ниже.
Номер фигуры \ (\ text {1} \) \ (\ text {2} \) \ (\ text {3} \) \ (\ text {4} \) \ (n \) Число точек Число строк Всего 75
Номер фигуры \ (\ text {1} \) \ (\ text {2} \) \ (\ text {3} \) \ (\ text {4} \) \ (n \) Количество точек \ (\ text {3} \) \ (\ text {4} \) \ (\ text {5} \) \ ( \ text {6} \) \ (n + 2 \) Количество строк \ (\ text {3} \) \ (\ text {5} \) \ (\ text {7} \) \ (\ text {9} \) \ (2n + 1 \) Итого \ (\ text {6} \) \ (\ text {9 } \) \ (\ text {12} \) \ (\ text {15} \) \ (3 (n + 1) \) Рассмотрим последовательность, показанную здесь: \ (- 4 \;; \; -1 \;; \; 2 \;; \; 5 \;; \; 8 \;; \; 11 \;; \; 14 \; ; \; 17 \;; \; \ ldots \)
Если \ (T_ {n} = \ text {2} \), каково значение \ (T_ {n-1} \)?
\ begin {align *}
T_ {3} & = \ text {2} \\
\ поэтому T_ {n-1} & = -1
\ end {выровнять *}Рассмотрим последовательность, показанную здесь: \ (C \;; \; D \;; \; E \;; \; F \;; \; G \;; \; H \;; \; I \;; \ ; J \;; \; \ ldots \)
Если \ (T_ {n} = G \), каково значение \ (T_ {n-4} \)?
\ begin {align *}
Т_ {5} & = G \\
\ поэтому T_ {n-4} & = C
\ end {выровнять *}\ (9 \;; \; -7 \;; \; -8 \;; \; -25 \;; \; -34 \;; \; \ ldots \)
\ begin {align *}
d & = T_ {2} – T_ {1} = (-7) – (9) = -16 \\
d & = T_ {3} – T_ {2} = (-8) – (-7) = -1 \\
d & = T_ {4} – T_ {3} = (-25) – (-8) = -17
\ end {выровнять *}Вы можете видеть, что результаты не совпадают – разница не обычная.Это означает, что эта последовательность чисел нелинейна, и у нее нет общей разницы.
\ (5 \;; \; 12 \;; \; 19 \; \; 26 \;; \; 33 \;; \; \ ldots \)
\ begin {align *}
d & = T_ {2} – T_ {1} = (12) – (5) = 7 \\
d & = T_ {3} – T_ {2} = (19) – (12) = 7 \\
d & = T_ {4} – T_ {3} = (26) – (19) = 7
\ end {выровнять *}Все результаты совпадают, что означает, что мы нашли общую разницу для этих чисел: \ (d = 7 \).
\ (\ text {2,93} \;; \; \ text {1,99} \;; \; \ text {1,14} \;; \; \ text {0,35} \;; \ ; \ ldots \)
\ begin {align *}
d & = T_ {2} – T_ {1} = \ left (\ text {1,99} \ right) – \ left (\ text {2,93} \ right) = – \ text {0,94} \ \
d & = T_ {3} – T_ {2} = \ left (\ text {1,14} \ right) – \ left (\ text {1,99} \ right) = – \ text {0,85}
\ end {выровнять *}В этом случае последовательность не является линейной.Поэтому окончательный ответ таков: общей разницы нет.
\ (\ text {2,53} \;; \; \ text {1,88} \;; \; \ text {1,23} \;; \; \ text {0,58} \;; \ ; \ ldots \)
\ begin {align *}
d & = T_ {2} – T_ {1} = \ left (\ text {1,88} \ right) – \ left (\ text {2,53} \ right) = – \ text {0,65} \ \
d & = T_ {3} – T_ {2} = \ left (\ text {1,23} \ right) – \ left (\ text {1,88} \ right) = – \ text {0,65}
\ end {выровнять *}Общее различие – \ (d = – \ text {0,65} \).
\ (5 \;; \; 15 \;; \; 25 \;; \; \ ldots \)
Общая разница:
\ begin {align *}
d & = T_ {2} – T_ {1} \\
& = 15 – 5 \\
& = 10
\ end {выровнять *}Поэтому мы добавляем \ (\ text {10} \) каждый раз, чтобы получить следующий член в последовательности. Следующие три числа:
.
\ (\ text {35} \), \ (\ text {45} \) и \ (\ text {55} \)
и последовательность становится:
\ (5 \;; \; 15 \;; \; 25 \;; \; 35 \;; \; 45 \;; \; 55 \;; \; \ ldots \)
\ (- 8 \;; \; -3 \;; \; 2 \;; \; \ ldots \)
Общая разница:
\ begin {align *}
d & = T_ {2} – T_ {1} \\
& = -3 – (-8) \\
& = 5
\ end {выровнять *}Поэтому мы добавляем \ (\ text {5} \) каждый раз, чтобы получить следующий член в последовательности.Следующие три числа:
.
\ (\ text {7} \), \ (\ text {12} \) и \ (\ text {17} \)
и последовательность становится:
\ (- 8 \;; \; -3 \;; \; 2 \;; \; 7 \;; \; 12 \;; \; 17 \;; \; \ ldots \)
\ (30 \;; \; 27 \;; \; 24 \;; \; \ ldots \)
Общая разница:
\ begin {align *}
d & = T_ {2} – T_ {1} \\
& = 27 – 30 \\
& = -3
\ end {выровнять *}Поэтому мы вычитаем \ (\ text {3} \) каждый раз, чтобы получить следующий член в последовательности.Следующие три числа:
.
\ (\ text {21} \), \ (\ text {18} \) и \ (\ text {15} \)
и последовательность становится:
\ (30 \;; \; 27 \;; \; 24 \;; \; 21 \;; \; 18 \;; \; 15 \;; \; \ ldots \)
\ (- \ text {13,1} \;; \; – \ text {18,1} \;; \; – \ text {23,1} \;; \ ldots \)
\ begin {align *}
d & = T_ {2} -T_ {1} \ text {или} T_ {3} -T_ {2} \\
& = (- \ text {18,1}) – (- \ text {13,1}) \ text {или} (- \ text {23,1}) – (- \ text {18,1}) \ \
& = – \ текст {5} \\
\ text {Следовательно} T_4 & = – \ text {28,1} \\
T_5 & = – \ text {33,1} \\
T_6 & = – \ text {38,1}
\ end {align *}\ (- 9 х \;; – 19 х \;; – 29 х \;; \ ldots \)
\ begin {align *}
d & = T_ {2} -T_ {1} \ text {или} T_ {3} -T_ {2} \\
& = (- 19 x) – (- 9 x) \ text {or} (- 29 x) – (- 19 x) \\
& = -10 х \\
\ text {Следовательно} T_4 & = – 39 x \\
Т_5 & = – 49 х \\
Т_6 & = – 59 х
\ end {align *}\ (- \ text {15,8} \;; \; \ text {4,2} \;; \; \ text {24,2} \;; \ ldots \)
\ begin {align *}
d & = T_ {2} -T_ {1} \ text {или} T_ {3} -T_ {2} \\
& = (\ text {4,2}) – (- \ text {15,8}) \ text {или} (\ text {24,2}) – (\ text {4,2}) \\
& = \ текст {20} \\
\ text {Следовательно} T_4 & = \ text {44,2} \\
T_5 & = \ text {64,2} \\
T_6 & = \ text {84,2}
\ end {align *}\ (30 б \;; 34 б \;; 38 б \;; \ ldots \)
\ begin {align *}
d & = T_ {2} -T_ {1} \ text {или} T_ {3} -T_ {2} \\
& = (34 b) – (30 b) \ text {или} (38 b) – (34 b) \\
& = 4 б \\
\ text {Следовательно} T_4 & = 42 b \\
Т_5 & = 46 б \\
T_6 & = 50 б
\ end {align *}Учитывая шаблон, который начинается с чисел: \ (3 \;; \; 8 \;; \; 13 \;; \; 18 \;; \; \ ldots \), определите значения \ (T_ {6} \) и \ (T_ {9} \).
\ [3 \; ; \; 8 \; ; \; 13 \; ; \; 18 \; ; \; 23 \; ; \; \ underline {28} \; ; \; 33 \; ; \; 38 \; ; \; \ underline {43} \; ; \; \ ldots \]
\ (T_ {6} = 28 \ text {и} T_ {9} = 43 \)
Учитывая последовательность, которая начинается с букв: \ (C \;; \; D \;; \; E \;; \; F \;; \; \ ldots \), определите значения \ (T_ {5} \) и \ (T_ {8} \).
\ [C \; ; \; D \; ; \; E \; ; \; F \; ; \; \ underline {G} \; ; \; H \; ; \; Я \; ; \; \ underline {J} \; ; \; \ ldots \]
\ (T_ {5} = G \ text {и} T_ {8} = J \)
Учитывая шаблон, который начинается с чисел: \ (7 \;; \; 11 \;; \; 15 \;; \; 19 \;; \; \ ldots \), определите значения \ (T_ {5} \) и \ (T_ {8} \).{2} – 1 \\
& = 16 – 1 \\
& = 15
\ end {выровнять *}Следовательно, отсутствует только третий член, то есть \ (\ text {8} \). Полная последовательность:
\ (0 \;; \; 8 \;; \; 15 \;; \; 24 \)
\ (3 \;; \; 2 \;; \; 1 \;; \; 0 \;; \; \ ldots; -2 \ qquad T_ {n} = -n + 4 \)
Пятый член:
\ begin {align *}
T_n & = -n + 4 \\
Т_ {5} & = – (5) + 4 \\
& = -1
\ end {выровнять *}Шестой член:
\ begin {align *}
T_n & = -n + 4 \\
Т_ {6} & = – (6) + 4 \\
& = -2
\ end {выровнять *}Следовательно, отсутствует только пятый член, то есть \ (- \ text {1} \).Полная последовательность:
\ (3 \;; \; 2 \;; \; 1 \;; \; 0 \;; \; -1 \;; \; -2 \)
\ (- 11 \;; \; \ ldots \; \; -7 \;; \; \ ldots \;; \; -3 \ qquad T_ {n} = -13 + 2n \)
Второй член:
\ begin {align *}
Т_н & = -13 + 2н \\
Т_ {2} & = -13 + 2 (2) \\
& = -13 + 4 \\
& = -9
\ end {выровнять *}Третий член:
\ begin {align *}
Т_н & = -13 + 2н \\
Т_ {3} & = -13 + 2 (3) \\
& = -13 + 6 \\
& = -7
\ end {выровнять *}Четвертый член:
\ begin {align *}
Т_н & = -13 + 2н \\
Т_ {4} & = -13 + 2 (4) \\
& = -13 + 8 \\
& = -5
\ end {выровнять *}Пятый член:
\ begin {align *}
Т_н & = -13 + 2н \\
Т_ {5} & = -13 + 2 (5) \\
& = -13 + 10 \\
& = -3
\ end {выровнять *}Следовательно, два пропущенных члена – это второй и четвертый термины: \ (- \ text {9} \) и \ (- \ text {5} \).Полная последовательность:
\ (- 11 \;; \; -9 \;; \; -7 \;; \; -5 \;; \; -3 \)
\ (\ text {1} \;; \; \ text {10} \;; \; \ text {19} \;; \; \ ldots \;; \; \ text {37} \ qquad T_n = 9 п – 8 \)
\ begin {align *}
Т_н & = 9 п – 8 \\
T_4 & = \ text {9} (\ text {4}) – \ text {8} \\
& = \ текст {28}
\ end {align *}\ (\ text {9} \;; \; \ ldots \;; \; \ text {21} \;; \; \ ldots \;; \; \ text {33} \ qquad T_n = 6 n + 3 \)
Чтобы найти два пропущенных члена, мы используем уравнение для общего члена:
\ begin {align *}
T_n & = \ text {6} n \ text {+3} \\
T_2 & = \ текст {6} (\ текст {2}) \ текст {+3} \\
& = \ текст {15} \\
T_4 & = \ text {6} (\ text {4}) \ text {+3} \\
& = \ текст {27}
\ end {align *}\ (2; 5; 8; 11; 14; \ ldots \)
Нам сначала нужно найти \ (d \):
\ begin {align *}
d & = T_ {2} – T_ {1} \\
& = 5 – 2 \\
& = 3
\ end {выровнять *}Далее отметим, что для каждого следующего члена мы добавляем \ (d \) к последнему члену.Мы можем выразить это как:
\ begin {align *}
Т_ {1} & = а = 2 \\
T_ {2} & = a + d = 2 + 3 \\
& = 2 + 1 (3) \\
Т_ {3} & = Т_ {2} + d = 2 + 3 + 3 \\
& = 2 + 2 (3) \\
Т_ {4} & = Т_ {3} + d = 2 + 3 + 3 + 3 \\
& = 2 + 3 (3) \\
T_ {n} & = T_ {n-1} + d = 2 + 3 (n-1) \\
& = 3n – 1
\ end {выровнять *}Общая формула \ (T_n = 3n – 1 \).
\ (T_ {10} \), \ (T_ {50} \) и \ (T_ {100} \):
\ begin {align *}
Т_ {10} & = 3 (10) – 1 \\
& = 29 \\
Т_ {50} & = 3 (50) – 1 \\
& = 149 \\
Т_ {100} & = 3 (100) – 1 \\
& = 299
\ end {выровнять *}\ (0; 4; 8; 12; 16; \ ldots \)
Нам сначала нужно найти \ (d \):
\ begin {align *}
d & = T_ {2} – T_ {1} \\
& = 4 – 0 \\
& = 4
\ end {выровнять *}Далее отметим, что для каждого следующего члена мы добавляем \ (d \) к последнему члену.Мы можем выразить это как:
\ begin {align *}
T_ {1} & = a = 0 \\
T_ {2} & = a + d = 0 + 4 \\
& = 4 (1) \\
Т_ {3} & = Т_ {2} + d = 0 + 4 + 4 \\
& = 4 (2) \\
Т_ {4} & = Т_ {3} + d = 0 + 4 + 4 + 4 \\
& = 4 (3) \\
T_ {n} & = T_ {n-1} + d = 0 + 4 (n-1) \\
& = 4n – 4
\ end {выровнять *}Общая формула \ (T_n = 4n – 4 \).
\ (T_ {10} \), \ (T_ {50} \) и \ (T_ {100} \):
\ begin {align *}
Т_ {10} & = 4 (10) – 4 \\
& = 36 \\
Т_ {50} & = 4 (50) – 4 \\
& = 196 \\
Т_ {100} & = 4 (100) – 4 \\
& = 396
\ end {выровнять *}\ (2; -1; -4; -7; -10; \ ldots \)
Нам сначала нужно найти \ (d \):
\ begin {align *}
d & = T_ {2} – T_ {1} \\
& = -1 – 2 \\
& = -3
\ end {выровнять *}Далее отметим, что для каждого следующего члена мы добавляем \ (d \) к последнему члену.Мы можем выразить это как:
\ begin {align *}
Т_ {1} & = а = 2 \\
T_ {2} & = a + d = 2 + (-3) \\
& = 2 + (-3) (1) \\
T_ {3} & = T_ {2} + d = 2 + (-3) + (-3) \\
& = 2 + (-3) (2) \\
T_ {4} & = T_ {3} + d = 2 + (-3) + (-3) + (-3) \\
& = 2 + (-3) (3) \\
T_ {n} & = T_ {n-1} + d = 2 + (-3) (n-1) \\
& = 5 – 3n
\ end {выровнять *}Общая формула \ (T_n = 5 – 3n \).{\ text {th}} \) изображение диаграммы.
\ begin {align *}
Т_ {п} & = 2n + 3 \\
T_ {25} & = 2 (25) + 3 \ longleftarrow \ text {replace n} = 25 \\
& = 53
\ end {align *}Запишите следующие \ (\ text {3} \) условия.
Отметим, что мы добавляем 8 к каждому члену, чтобы получить следующий член. Следовательно, следующие три члена – это \ (47 \;; \; 55 \;; \; 63 \).
Найдите общую формулу последовательности
\ begin {align *}
T_n & = T_1 + d (n – 1) \\
& = 15 + 8 (п-1) \\
& = 8n + 7
\ end {выровнять *}Найдите значение \ (n \), если \ (T_n \) равно \ (\ text {191} \).
\ begin {align *}
191 & = 8n + 7 \\
184 & = 8n \\
n & = 23
\ end {выровнять *}Запишите следующие \ (\ text {3} \) условия.
Отметим, что мы добавляем 30 к каждому члену, чтобы получить следующий член. Следовательно, следующие три члена – это \ (76 \;; \; 106 \;; \; 136 \).
Найдите общую формулу последовательности
\ begin {align *}
T_n & = T_1 + d (n – 1) \\
& = -44 + 30 (п – 1) \\
& = 30n -74
\ end {выровнять *}Найдите значение \ (n \), если \ (T_n \) равно \ (\ text {406} \).
\ begin {align *}
406 & = 30н – 74 \\
480 & = 30n \\
n & = 16
\ end {выровнять *}Найдите общее различие для терминов списка. Если последовательность не линейная (если у нее нет общей разницы), напишите «нет общей разницы».
\ begin {align *}
d & = T_ {2} – T_ {1} = (- 4 z – 5) – (- z – 5) = – 3 z \\
& = T_ {3} – T_ {2} = (- 6 z – 2) – (- 4 z – 5) = – 2 z + 3 \\
& = T_ {4} – T_ {3} = (- 8 z – 5) – (- 6 z – 2) = – 2 z – 3
\ end {выровнять *}
Нет общей разницы.Если вам теперь говорят, что \ (z = -2 \), определите значения \ (T_ {1} \) и \ (T_ {2} \).
\ begin {align *}
Т_ {1} & = – z – 5 \\
& = – (-2) -5 \\
& = -3 \\
Т_ {2} & = – 4 z – 5 \\
& = – 4 (-2) -5 \\
& = 3
\ end {align *}Найдите общую разницу для членов шаблона.Если последовательность не линейная (если у нее нет общей разницы), напишите «нет общей разницы».
\ begin {align *}
d & = T_ {2} – T_ {1} = (1) – (2n + 4) = – 2n – 3 \\
& = T_ {3} – T_ {2} = (- 2n – 2) – (1) = – 2n – 3 \\
& = T_ {4} – T_ {3} = (- 4n – 5) – (- 2n – 2) = – 2n – 3
\ end {выровнять *}
Общая разница для этих чисел: \ (d = – 2n – 3 \).Если вам теперь говорят, что \ (n = -1 \), определите значения \ (T_ {1} \) и \ (T_ {3} \).
\ begin {align *}
Т_ {1} & = 2 п + 4 \\
& = 2 (-1) +4 \\
& = 2 \\
Т_ {3} & = – 2 п – 2 \\
& = – 2 (-1) -2 \\
& = 0
\ end {align *}Если следующие члены образуют линейную последовательность:
\ [\ frac {k} {3} – 1 \; ; \; – \ frac {5k} {3} + 2 \; ; \; – \ frac {2k} {3} + 10 \; ; \; \ ldots \]Определите значение \ (k \).Если ответ не целое число, запишите ответ в виде упрощенной дроби.
\ begin {align *}
T_ {2} – T_ {1} & = T_ {3} – T_ {2} \\
\ left (- \ frac {5k} {3} + 2 \ right) – \ left (\ frac {k} {3} – 1 \ right) & = \ left (- \ frac {2k} {3} + 10 \ right) – \ left (- \ frac {5k} {3} + 2 \ right) \\ \\
3 \ left (- \ frac {5k} {3} + 2 \ right) – 3 \ left (\ frac {k} {3} – 1 \ right) & = 3 \ left (- \ frac {2k} {3 } + 10 \ right) – 3 \ left (- \ frac {5k} {3} + 2 \ right) \\
– 5k + 6 – \ left (k – 3 \ right) & = – 2k + 30 – \ left (- 5k + 6 \ right) \\
– 6к + 9 & = 3к + 24 \\
-15 & = 9к \\
k & = – \ frac {5} {3}
\ end {align *}Теперь определите числовое значение первых трех членов.Если ответы не являются целыми числами, запишите их дробными числами.
\ begin {align *}
\ text {Первый член:} T_ {1} & = \ frac {k} {3} – 1 \\
& = \ frac {\ left (- \ frac {5} {3} \ right)} {3} -1 \\
& = – \ frac {14} {9} \\
\ text {Второй член:} T_ {2} & = – \ frac {5 k} {3} + 2 \\
& = – \ frac {5 \ left (- \ frac {5} {3} \ right)} {3} +2 \\
& = \ frac {43} {9} \\
\ text {Третий член:} T_ {3} & = – \ frac {2 k} {3} + 10 \\
& = – \ frac {2 \ left (- \ frac {5} {3} \ right)} {3} +10 \\
& = \ frac {100} {9}
\ end {выровнять *}
Первые три члена этой последовательности: \ (- \ frac {14} {9}, \ frac {43} {9} \) и \ (\ frac {100} {9} \).Если следующие члены образуют линейную последовательность:
\ [y – \ frac {3} {2} \; ; \; – у – \ frac {7} {2} \; ; \; – 7 лет – \ frac {15} {2} \; ; \; \ ldots \]найти \ (y \). Если ответ не целое число, запишите ответ в виде упрощенной дроби.
\ begin {align *}
T_ {2} – T_ {1} & = T_ {3} – T_ {2} \\
\ left (- y – \ frac {7} {2} \ right) – \ left (y – \ frac {3} {2} \ right) & = \ left (- 7 y – \ frac {15} {2 } \ right) – \ left (- y – \ frac {7} {2} \ right) \\ \\
2 \ left (- y – \ frac {7} {2} \ right) – 2 \ left (y – \ frac {3} {2} \ right) & = 2 \ left (- 7y – \ frac {15} {2} \ right) – 2 \ left (- y – \ frac {7} {2} \ right) \\
– 2y – 7 – \ left (2y – 3 \ right) & = – 14y – 15 – \ left (- 2y – 7 \ right) \\
– 4л – 4 & = – 12л – 8 \\
8лет & = -4 \\
y & = – \ frac {1} {2}
\ end {align *}Теперь определите числовое значение первых трех членов.Если ответы не являются целыми числами, запишите их дробными числами.
\ begin {align *}
\ text {Первый член:} T_ {1} & = y – \ frac {3} {2} \\
& = \ left (- \ frac {1} {2} \ right) – \ frac {3} {2} \\
& = -2 \\
\ text {Второй член:} T_ {2} & = – y – \ frac {7} {2} \\
& = – \ left (- \ frac {1} {2} \ right) – \ frac {7} {2} \\
& = -3 \\
\ text {Третий член:} T_ {3} & = – 7 y – \ frac {15} {2} \\
& = – 7 \ left (- \ frac {1} {2} \ right) – \ frac {15} {2} \\
& = -4
\ end {выровнять *}
Первые три члена этой последовательности: \ (- 2, -3 \ text {и} -4 \).{\ text {th}} \) буква в слове, то есть EЧисловые шаблоны | Учебные идеи
2D искусство
2D форма
Сложение и вычитание
Энди Голдсуорси
Углы
Область
Сборки, связанные с событиями
Оценка
легкая атлетика
Ресурсы для авторов
Ресурсы по аутизму
Средние
Поход
христианство
Цвета на языках
Запятые
Сравнение и заказ
Состав
Союзы и связки
Технология управления
Режущие и ножничные навыки
Ежедневные наполнители
Развитие уверенности
Удвоение
Нарисуйте мультфильм
Эмоции
Энергия
Эксперименты и исследования
Французские числа
Немецкие номера
Грамматика
Греческие цвета
Исторические источники
Омофоны
Линия в искусстве
Литовские номера
Магниты
Микроорганизмы
Число
Абзацы
Место значение
Истории планирования
Инструкции по чтению
Воспоминания
Ресурсы для вознаграждений
Скалы и почвы
Навыки социальных сетей
Знакомство с испанским
Особые потребности
Написание
Симметрия и отражение
Каменный век
Вулканы
Идеи для разогрева
Написание текстов для обсуждения
3D искусство
3D форма
Энди Уорхол
Животные и среда обитания
Ацтеки
Ресурсы BoardMaker
Вместимость
Празднование Дней Рождения
Танец
Базы данных
Словарные навыки
Нарисуйте фото
Сборки в конце года
Английские тайм-наполнители
Оценка
Полевые работы
Французские цвета
Полные остановки и заглавные буквы
Геометрия
Немецкие цвета
Хорошие отношения
Графики
Греческие числа
Группировка материалов
Почерк
индуизм
Инструменты
Литовские цвета
Забота о деньгах
Умножение и деление
Существительные Прилагательные Глаголы и наречия
Числовые узоры
Числа на языках
Парашютная деятельность
Узор и симметрия в искусстве
Периметр
Пунктуация
Чтение отчетов
Примечания к награде
Школьная форма
Испанские числа
Орфографические шаблоны
Сюжетные персонажи
Железный век
Наполнители времени
Таблицы умножения
Написание объяснений
Добавление
Площадь и периметр
Сборки, связанные с предметами
Бриджит Райли
Великобритания с 1948 года
Смена материалов
Цепи и электричество
Обратный отсчет в классе
Классное руководство
Цвет
Ресурсы для рисования
Ресурсы по диспраксии
Оценка времени наполнителей
Факторы
Футбол и футбол
Игры
Глобальная география
Здоровый образ жизни
Деятельность на сотнях квадратных метров
Редактирование изображений
Кавычки
ислам
Умение слушать
Мера
Вероятность
Вопросительные слова
Чтение
Чтение художественной литературы
Чтение убедительного письма
Идеи вознаграждения
Язык знаков
Пространство в искусстве
Испанские праздники и особые случаи
Советы и идеи по правописанию
Настройки истории
Бронзовый век
Написание художественной литературы
Инструкции по написанию
Сборки
Награды в классе
Рисование и зарисовки
Ранняя история человечества
Земля и за ее пределами
Фрэнк Стелла
Французский
Иудаизм
Местная география
Заполнители времени для математики
Ментальные стартеры
Мультимедиа
Музыкальные элементы
Отрицательные числа
Активная роль
Вопросительные знаки
Чтение научно-популярной литературы
Сортировка
Испанские цвета
Виды спорта
Идеи для написания рассказов
Вычитание
Суффиксы и префиксы
Плавание
Синонимы и антонимы
Объем
Письмо
Написание научно-популярной литературы
Написание убедительного письма
Идеи остывания
Координаты
Показать советы и ресурсы
Египтяне
Элементы искусства
Силы
Немецкий
Кандинский
Карты и атласы
Заполнители времени памяти
Умножение
Обозначение
Нечетный и четный
Решение проблем
Чтение стихов
Сикхизм
Испанская еда и напитки
Говорить и слушать
Спортивный день
Таблицы
Слова, связанные с речью
Писать стихи
Написание отчетов
Разделение
Завершить картину
Отделочные работы
Греческий
Греки
Гимнастика
Человеческая биология
Длина
Лоури
Горы
Наполнители времени головоломки
Размышляя о чтении
Округление
Испанское время
Статистика
Интернет
Словарь
Написание отчетов
Все четыре операции
Привлечение внимания
Учимся у художников и о них
Свет
Литовский
Масса и вес
майя
Моне
Стихийные бедствия
Погода в Испании
Большой теннис
Обработка текста
Фракции
Управление перерывами
Материалы
Пикассо
Реки
Римляне
испанский
Испанские животные
Время
Десятичные дроби
Передвигаться
Растения
Тюдоры
Урду
Ван Гог
Воды
Проценты
Планирование
Звук
Викторианцы
Погода
Соотношение и пропорции
Ресурсы школьного клуба
Викинги
Деньги
Уборка
Мировая война 1
Алгебра
Переходные мероприятия
Вторая мировая война
Головоломки с картинками
Работа с родителями
Акустика
Изобразительное искусство
Вычисление
DT
английский
География
История
Языки
Математика
Музыка
Другие темы
PE
PSHE
RE
Наука
Как искать закономерности в числах
Целью математической игры, которую мы начали в прошлый раз, было выяснить, что происходит, когда мы складываем положительные нечетные целые числа.Чтобы решить эту головоломку, мы начали с рассмотрения последовательности чисел, которые мы получаем, когда складываем первое 1 положительное нечетное целое число (которое является просто числом 1), а затем первые 2 положительных нечетных целых числа (что составляет 1 + 3 = 4 ), затем первые 3 положительных нечетных целых числа (что равно 1 + 3 + 5 = 9) и так далее до бесконечности … и так далее. Конечно, мы остановились задолго до того, как достичь вечности (иначе мы бы все равно продолжили), и после еще нескольких проблем со сложением мы обнаружили, что сложение увеличивающихся чисел положительных нечетных целых чисел дает последовательность: 1, 4, 9, 16 , 25, 36, 49 и т. Д.
Но что с того? Почему мы это сделали? Конечно, наша настоящая цель состояла в том, чтобы «доказать» себе, нашим друзьям и всему миру, что математика – не ужасный ботаник (что мы закончим на следующей неделе). Но пока я хотел бы сосредоточиться на том факте, что найденная последовательность чисел приводит к нескольким интересным вопросам. А именно, сможете ли вы найти в последовательности узор? И если вы сможете найти шаблон, сможете ли вы также выяснить, почему этот шаблон существует? Именно об этом мы и поговорим сегодня.
Что такое узоры в числах?
Как я упоминал в прошлый раз, замечательно, если вы видите последовательность чисел, например, 1, 4, 9, 16, 25, 36, 49 и т. Д., И сразу видите закономерность. Но не беспокойтесь, если вы этого не сделаете. На самом деле, чтобы научиться замечать подобные вещи, нужно время и практика. Итак, заметили ли вы закономерность в этих числах или нет, давайте потратим несколько минут на то, чтобы пройти через процесс, который я мог бы предпринять, чтобы ее найти.
Первое, что вы можете заметить в последовательности 1, 4, 9, 16, 25, 36, 49, – это то, что все числа становятся все больше и больше.Это шаблон? Конечно. Но интересно ли это? Другими словами, можно ли его использовать, чтобы выяснить, каким должно быть следующее число в последовательности – раз это то, что нас здесь действительно интересует. В данном случае не совсем. В конце концов, мы создали последовательность, в первую очередь, сложив все большие и большие положительные целые числа. Так что сумма обязательно должна увеличиваться. Это означает, что хотя это своего рода шаблон, он не особенно интересен.
Значение ошибок в математике
Поскольку я очень разборчив в шаблонах, давайте попробуем найти что-нибудь более проницательное.Как насчет разницы между числами? Другими словами, получаете ли вы одно и то же число каждый раз, когда вычитаете одно число в последовательности из следующего? А может получится какой-нибудь другой интересный результат? Давай попробуем и посмотрим. Первые несколько различий между числами в последовательности: 4 – 1 = 3, 9 – 4 = 5 и 16 – 9 = 7. Таким образом, различия не все одинаковы (что кажется интересным), и похоже, что они следуют шаблону (что тоже кажется довольно интересным). Теперь нам нужно спросить себя, действительно ли это проницательная закономерность, которую мы обнаружили? К сожалению, когда мы это делаем, мы видим, что это не так.Фактически, мы видим, что просто (и как бы глупо) заново открыли последовательность положительных нечетных чисел – 3, 5, 7 и так далее, – которые мы использовали для создания нашего списка в первую очередь. Хотя вы можете утверждать, что это знание позволяет вам предсказать следующее число в последовательности, это не новая информация. А значит, и не очень информативный.
Это подводит нас к важному уроку: математика – это процесс, который должен быть полон глупых ошибок. В совершении ошибок нет ничего плохого, так что не бойтесь пробовать что-нибудь.Чаще всего первое, что вы попробуете, окажется неправильным, как это часто бывает, когда я решаю математические задачи для своих астрономических исследований. Но попытки сделать что-то неправильное – это первый шаг к открытию правильных вещей. И поскольку мы пока пытались решить нашу головоломку не так, как надо, мы все еще ищем выигрышный паттерн. Так что еще мы можем найти?
Попытки сделать неправильные вещи – это первый шаг к открытию правильных вещей.
Как искать закономерности в числах
Чтобы по-новому взглянуть на нашу головоломку, давайте попробуем совершенно другой такт: представьте, что у вас есть несколько групп блоков.Помимо одиночного блока, у вас также есть три других группы блоков, расположенных по прямым линиям: цепочка из 4 блоков, цепочка из 9 блоков и цепочка из 16 блоков. Вам знакомы эти числа – 1, 4, 9 и 16? К настоящему времени они должны это сделать, поскольку это первые четыре числа в нашей последовательности. Так как же эти цепочки блоков помогут нам найти закономерность в наших числах?
Представьте, что блоки в каждой нити скреплены резинкой, так что вы можете перемещать их и изменять их общую форму.Например, вы можете взять прядь из 4 блоков, которые расположены по прямой линии, и переместить 1 блок, чтобы превратить прядь в своего рода L-образную форму. И если вы подумаете об этом, вы увидите, что вы также можете взять прямые 4, 9 и 16 блочные пряди, немного переставить их и сложить каждую в идеальный квадрат – 4-блочная прядь станет 2×2 квадрат, нить из 9 блоков станет квадратом 3×3, а нить из 16 блоков станет квадратом 4×4.
Тайна идеальных квадратов
Это означает, что первые четыре числа в нашей последовательности можно сложить в полные квадраты.Это не только «интересно», я бы сказал, что это невероятно интересно, потому что большинство существующих чисел нельзя сложить в такие квадраты. И все же хоть один из наших может быть! Шаблон продолжает работать? Другими словами, является ли каждое число в нашем списке квадратом некоторого числа? Итак, следующее число в списке 25, а 25 равно 5×5. Так что да, этот тоже работает. Число после этого – 36, что составляет 6×6, и если вы продолжите идти, вы обнаружите, что этот узор продолжает сохраняться … навсегда!
Что-нибудь из этого кажется вам странным? В конце концов, мы начали с того, что просто сложили положительные нечетные числа.И мы каким-то образом закончили тем, что создали список всех очень особых чисел, известных как полные квадраты – 1, 4, 9, 16 и так далее. Если задуматься на минуту, это еще более странно, ведь почему сложение нечетных чисел имеет какое-либо отношение к созданию идеальных квадратов? Они кажутся совершенно разными зверями! Здесь что-то сверхглубокое? Теперь, когда мы обнаружили закономерность, мы, наконец, готовы ответить на этот вопрос и выяснить, почему он существует.
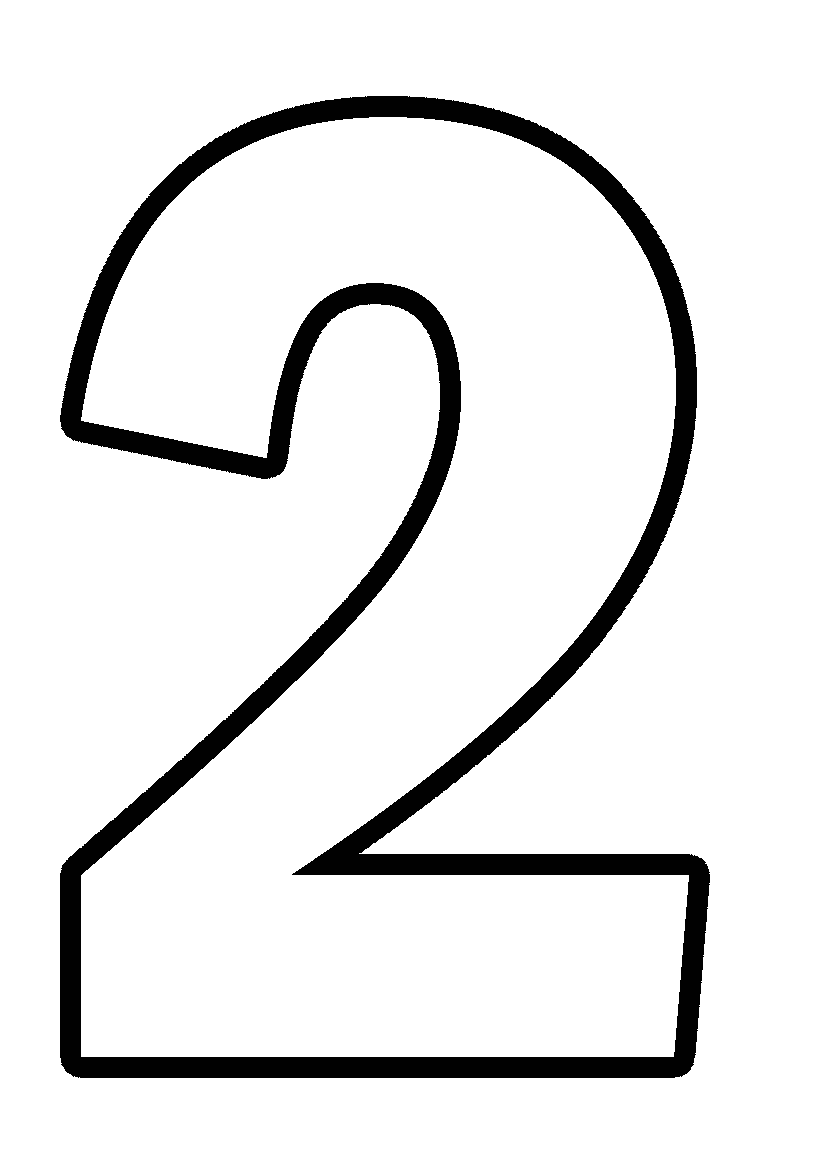 л. сахара
л. сахара
:max_bytes(150000):strip_icc()/NUMBERS-10-56a80f0e5f9b58b7d0f045f6.png) Например, торт-цифра состоит из коржей, вырезанных по готовому шаблону. Его можно распечатать или начертить самому. На корж кладут трафарет и обрезают лишние края. Готовые восьмерки выпекают и украшают.
Например, торт-цифра состоит из коржей, вырезанных по готовому шаблону. Его можно распечатать или начертить самому. На корж кладут трафарет и обрезают лишние края. Готовые восьмерки выпекают и украшают. Канцелярским ножом убирают погрешности.
Канцелярским ножом убирают погрешности.

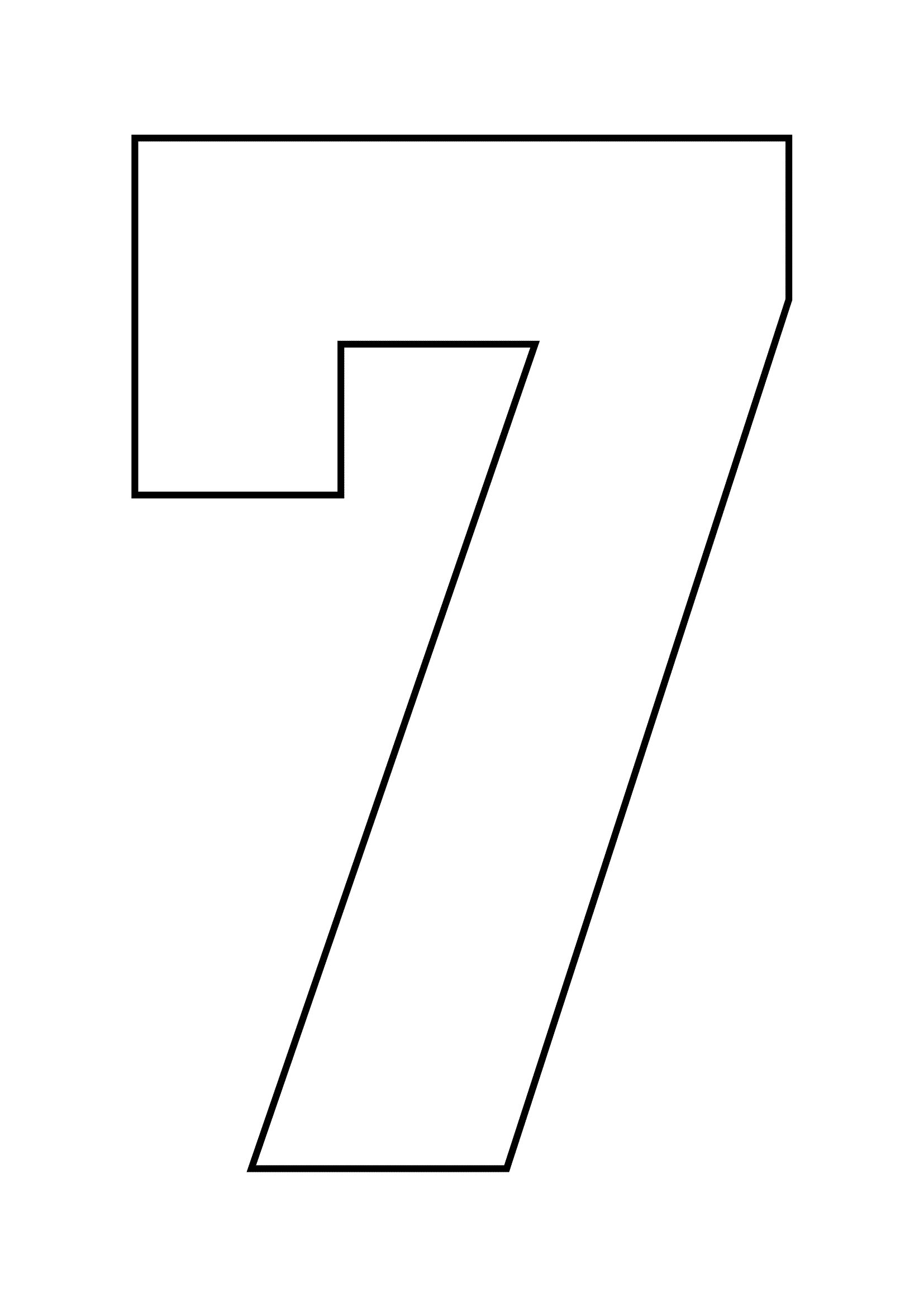

 Делаю это для того, чтобы следы от карандаша остались на изнаночной стороне, а не на лицевой.
Делаю это для того, чтобы следы от карандаша остались на изнаночной стороне, а не на лицевой. Для большого количества циферок, планируемых использоваться как реквизит для фотосессии, лучше предпочесть толстый картон А4. если в планах огромные поделки, придется проявить изобретательность и отыскать большие коробки от крупной бытовой техники. Проще всего это сделать, спросив в магазине: обычно продавцы с радостью отдают ненужные упаковки от товара.
Для большого количества циферок, планируемых использоваться как реквизит для фотосессии, лучше предпочесть толстый картон А4. если в планах огромные поделки, придется проявить изобретательность и отыскать большие коробки от крупной бытовой техники. Проще всего это сделать, спросив в магазине: обычно продавцы с радостью отдают ненужные упаковки от товара.
 Шаблоны даны ниже.
Шаблоны даны ниже.





 {3}; \ ldots \) и посмотрите узор с полномочиями. Вы можете обсудить это в классе как предшественник геометрических рядов, которые будут представлены в 12 классе.
{3}; \ ldots \) и посмотрите узор с полномочиями. Вы можете обсудить это в классе как предшественник геометрических рядов, которые будут представлены в 12 классе. {\ text {th}} \) и записывается как \ ({T} _ {n} \).{\ text {th}} \) член определяется общей формулой:
{\ text {th}} \) и записывается как \ ({T} _ {n} \).{\ text {th}} \) член определяется общей формулой: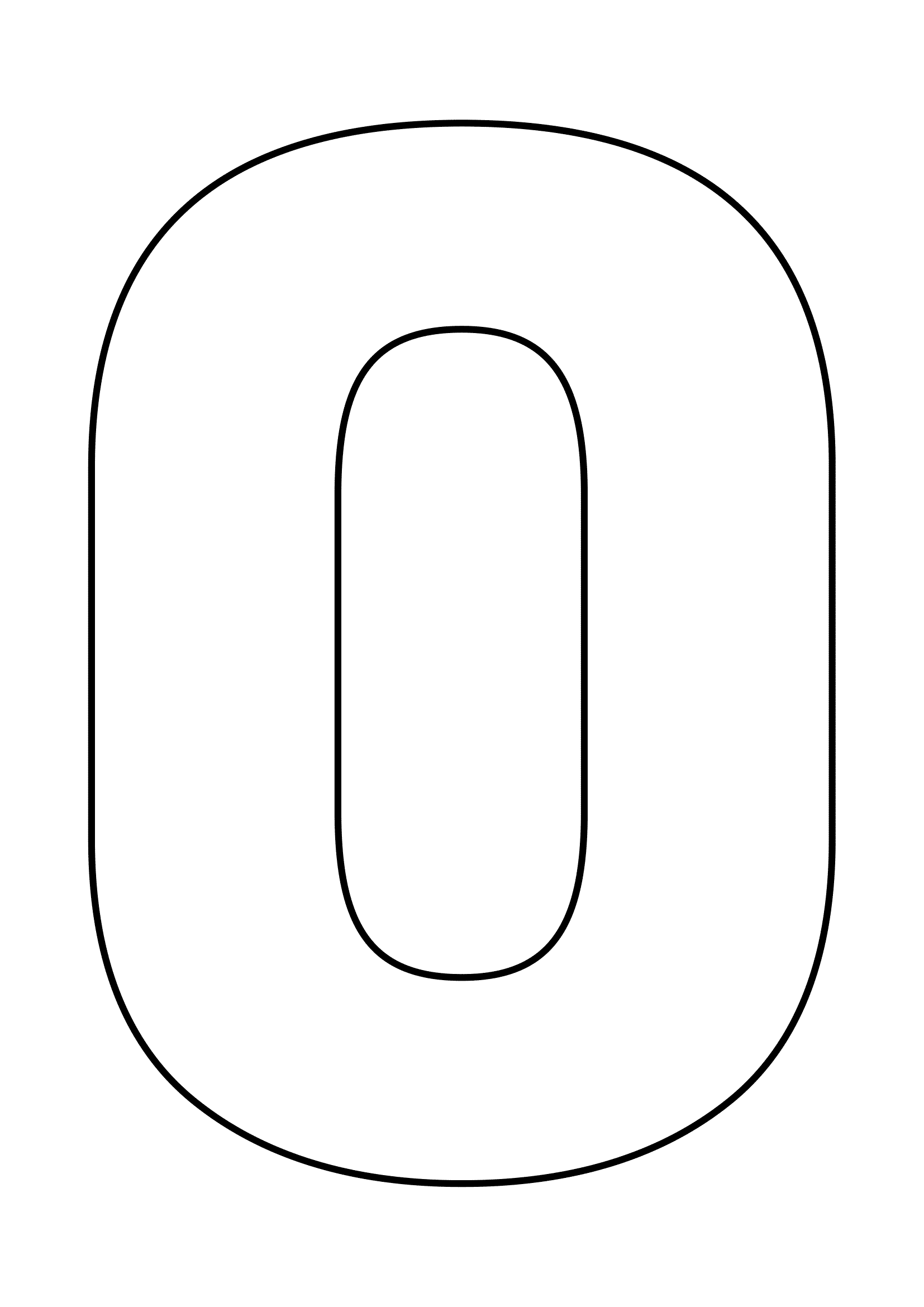 Это называется общей разницей .
Это называется общей разницей .