Разные фигуры геометрические: Основные геометрические фигуры 🟢🟨🔺 и их названия

Основные геометрические фигуры

Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. Где же встречаются геометрические фигуры в нашей жизни?

Где встречаются геометрические фигуры в нашей жизни?

Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. 

Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

И в современном мире без этих знаний не прожить.

Где же встречаются геометрические фигуры в нашей жизни?

Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды. К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр. 

Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия. Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте. 

Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах. Кроме того, интерактивные задания красочные, интересные, увлекательные.

Итак,

Простейшие виды фигур

Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.

Точка

Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик. Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом. Например, A, B, C или 1, 2, 3.

Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.

Самыми простейшими фигурами являются луч и отрезок.

• ^{Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.}
• ^{Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.}

Линия

Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными. 

• ^{Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.}
• ^{Разомкнутая — когда начало и окончание линии не соединены.}
• ^{Прямая — непрерывная линия без изменений.}
• ^{Кривая — отличная от прямой линии.}
• ^{Ломаная — когда соединены отрезки не под углом 180 градусов.} 

Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.

Основные геометрические фигуры

Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости. 

Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.

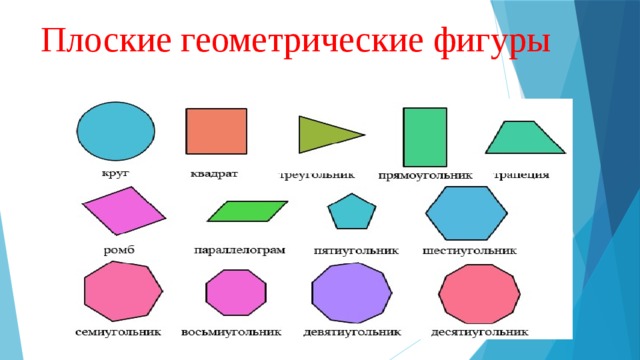
Если все точки фигуры находятся в одной плоскости, значит, она является плоской. Плоские фигуры, которые знают все: точка, квадрат, прямоугольник, треугольник, круг, полукруг, окружность, овал, ромб, трапеция.

А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.

Разберём плоские фигуры.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

 Есть три вида треугольников:

• ^{Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.}
• ^{Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.}
• ^{Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.}

Треугольники имеют следующие свойства:

• ^{в треугольнике напротив большего угла лежит большая сторона и наоборот;}
• ^{сумма углов треугольника всегда равна 180 градусам;}
• ^{все углы равностороннего треугольника равны 60 градусам;}
• ^{в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).}

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.

Примеры треугольников:

Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии. 

 

Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.

‍

Прямоугольник

‍

Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:

• ^{противоположные стороны равны между собой;}
• ^{диагонали равны и делятся в точке пересечения пополам;}
• ^{около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.}

‍

Квадрат

Квадрат — это тот же прямоугольник, у которого:

• ^{все стороны равны;}
• ^{все углы равны и составляют 90 градусов;}
• ^{диагонали равны и перпендикулярны;}
• ^{центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.}

‍

Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность. 

‍

Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.

Параллелограмм имеет следующие свойства:

• ^{противоположные стороны и углы равны;}
• ^{сумма двух любых соседних углов равна 180 градусам;}
• ^{диагонали пересекаются и точкой пересечения делятся пополам;}
• ^{каждая диагональ делит фигуру на два равных треугольника.}

Основные величины и их формулы

Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.

Периметр

Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

Обозначается заглавной латинской P.

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь. 

‍

На рисунке площади фигур окрашены различными цветами.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм², см², м², км² и т. д. S (square) — знак площади.

Вычисление периметра и площади

Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.

• ^{Квадрат: периметр = 4 * сторона.}
• ^{Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.}
• ^{Неправильный многоугольник: периметр = сумме всех сторон многоугольника.}
• ^{Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).}

Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:

• ^{Параллелограмм: площадь = основание * высота}
• ^{Квадрат: площадь = сторона 1 * сторона 2}
• ^{Треугольник: площадь = ½ * основание * высота}
• ^{Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).}

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:

• ^{интерактивные задания больше похожи на игру;}
• ^{их можно отрабатывать многократно и они не будут повторяться;}
• ^{платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;}
• ^{достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.}

Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.

Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Виды геометрических фигур | Бери и Делай

02.09.2021

Множество точек дает линию, а из нескольких соединенных между собой линий можно получить различные геометрические фигуры на плоскости и в пространстве. Таким образом, произвольное множество точек позволяет нам создавать геометрическую фигуру. Это может быть квадрат или куб, круг или шар, а также более сложные и неоднозначные фигуры, например икосаэдр, который может быть представлен двумя разными формами.

«Бери и Делай» предлагает узнать, чем отличаются разные виды геометрических фигур.

Плоские геометрические фигуры

Плоская геометрическая фигура располагается в двумерном пространстве, где объекты характеризуются только длиной и шириной. Различают следующие фигуры:

• Круг — это фигура, у которой нет углов и в которой все точки по окружности находятся на равном расстоянии от центра.
• Овал — это фигура, похожая на яйцо. У нее также нет углов.
• Квадрат — это фигура, у которой 4 равные стороны и 4 прямых угла.
• Прямоугольник — это фигура, похожая на квадрат: у нее 4 стороны и они пересекаются под прямым углом. В отличие от квадрата, у прямоугольника только противолежащие стороны равны. Если с помощью отрезка соединить любой угол с противоположным, получится диагональ. И у квадрата, и у прямоугольника диагонали равны.
• Ромб — это фигура, у которой 4 равные стороны, но пересекаются они не под прямыми углами. У ромба противоположные углы ромба равны. Ромб, так же как квадрат и прямоугольник, является четырехугольником.
• Треугольник — это фигура, у которой 3 угла и 3 стороны. Точки, в которых пересекаются стороны треугольника, принято называть его вершинами.

Виды треугольников в зависимости от размера углов: 🔷 остроугольный — все углы острые (каждый равен менее 90°) 🔷 тупоугольный — один угол является тупым (равным более 90°) 🔷 прямоугольный — один угол является прямым (равным 90°)

Различают также виды треугольников по соотношению их сторон: 🔶 равносторонний имеет 3 равные стороны 🔶 равнобедренный — 2 равные стороны 🔶 разносторонний — 3 разные стороны

Выше мы рассмотрели основные геометрические фигуры на плоскости. Но существует множество других, например:

• Трапеция — это четырехугольник, у которого как минимум 2 стороны параллельны. Таким образом, квадрат, ромб и прямоугольник можно рассматривать как частные случаи трапеции.
• Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны. Так, прямоугольник, квадрат и ромб считаются частными случаями параллелограмма.
• Пентагон — фигура, представляющая собой правильный многоугольник с 5 сторонами. У пентагона все стороны и углы равны.
• Гексагон — это правильный многоугольник, у которого 6 равных сторон, а углы образуют 6 равносторонних треугольников.
• Крест — это фигура, которая состоит из 2 пересекающихся линий или прямоугольников.
• Звезда — плоский невыпуклый многоугольник, по форме напоминающий звезду. Звезда может быть трехконечной, четырехконечной, пятиконечной (как на картинке выше) и так далее.

Геометрическая фигура может быть выпуклой, если ей целиком принадлежат все точки отрезка, соединяющего любые ее две точки. Круг, шар, овал и треугольник являются выпуклыми фигурами. А четырехугольники могут быть как выпуклыми, так и невыпуклыми. К примеру, на картинке выше изображена одна и та же фигура — дельтоид. Это четырехугольник, стороны которого можно сгруппировать в две пары равных смежных сторон. Слева — дельтоид выпуклый, а справа — невыпуклый.

Пространственные геометрические фигуры

Если фигура располагается в трехмерном пространстве, где объекты характеризуются длиной, шириной и высотой, а также имеют глубину или толщину, ее называют пространственной. Чаще всего различают следующие пространственные фигуры:

• Шар можно назвать аналогом круга в пространстве. Все точки, располагающиеся на поверхности шара, находятся на равном расстоянии от его центра.
• Конус образован множеством лучей, которые соединяют все точки некоторой плоской кривой с единой точкой пространства (вершиной конуса). Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус.
• Цилиндр по своей форме напоминает валик. В его основании находятся круги, а между ними — часть цилиндрической поверхности.
• Куб — это многогранная фигура, каждая грань которой представляет собой квадрат. При этом у него 6 граней, 12 ребер и 8 вершин. Куб также можно назвать правильным гексаэдром, или шестигранником.
• Пирамида — это многогранник, у которого в основании находится многоугольник, а грани представлены треугольниками, имеющими общую вершину.
• Призма — это многогранник, 2 грани которого являются равными многоугольниками, располагающимися в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. На картинке выше частный пример — шестиугольная призма. У нее 8 граней, 18 ребер и 12 вершин.

Если выпуклый многогранник состоит из одинаковых правильных многоугольников и обладает пространственной симметрией, то его называют правильным многогранником, или платоновым телом. В трехмерном пространстве различают 5 таких правильных многогранников. Название каждого из них происходит от греческого наименования количества его граней:

• Тетраэдр, или треугольная пирамида. У этого многогранника гранями являются 4 треугольника.
• Гексаэдр, или куб.
• Октаэдр — многогранник, чьими гранями являются 8 равносторонних треугольников. Если разрезать октаэдр пополам, можно получить две одинаковые пирамиды.
• Додекаэдр — многогранник, у которого 12 граней и все они правильные пятиугольники.
• Икосаэдр — многогранник, гранями которого являются 20 правильных треугольников.

При этом правильный икосаэдр может быть как выпуклым, так и невыпуклым. Но термин «правильный икосаэдр» чаще относится к выпуклому виду, а невыпуклая форма называется большим икосаэдром.

Поделиться в социальных сетях

Вам может понравиться

Геометрические фигуры — определение, список, типы, свойства

Любой объект вокруг нас с фиксированной структурой можно считать геометрической формой. Эти формы состоят из линий, кривых, углов и поверхностей. Некоторыми из известных геометрических фигур являются квадрат, прямоугольник, круг, цилиндр и т. д. Многоугольник — это геометрическая форма с 3 или более сторонами. Некоторые из распространенных многоугольников: треугольник, квадрат, ромб, трапеция и т. д.

В этой статье мы рассмотрим различные двухмерные и трехмерные геометрические фигуры и их свойства. На их основе мы решим несколько примеров для лучшего понимания концепции.

1.	Что такое геометрические фигуры?
2.	Типы геометрических фигур
3.	Список и свойства геометрических фигур
4.	Часто задаваемые вопросы о геометрических фигурах

Что такое геометрические фигуры?

Геометрические фигуры – это любая структура, открытая или замкнутая, имеющая определенную форму и свойства, состоящая из линий, кривых и точек. Некоторыми из известных геометрических фигур являются квадрат, прямоугольник, круг, конус, цилиндр, сфера и т. д. Все эти формы обладают некоторыми свойствами, которые делают их уникальными и отличными от других форм.

Геометрические фигуры определяются как фигуры, замкнутые границей, которая образована путем объединения определенного количества кривых, точек и отрезков. Каждая фигура имеет уникальное имя, такое как круг, квадрат, треугольник, прямоугольник и т. д. В реальной жизни нас окружают различные основные геометрические фигуры, например, кусок пиццы имеет форму треугольника, двери или окна в форме треугольника. форма прямоугольника и многое другое.

Типы геометрических фигур

В геометрии, когда объект или фигура не соединены с обоих концов, это считается открытой геометрической формой. Когда объект или форма соединены с обоими концами, это считается замкнутой геометрической формой. Существует два типа геометрических фигур, которые классифицируются как:

• Двумерные: Это двумерные фигуры, которые имеют только оси x и y. Это плоские структуры с 2 измерениями. Например, треугольник, квадрат, прямоугольник и т. д.
• Трехмерный: Это трехмерные фигуры, которые имеют оси x, y и z. Ось Z представляет высоту объекта. Это твердые структуры с 3 измерениями. Например, куб, прямоугольный параллелепипед и т. д.

Чтобы нарисовать любую из этих геометрических фигур, мы должны начать с линии, кривой или отрезка. Таким образом, на основе количества и расположения линий мы можем создавать различные типы геометрических фигур и фигур, например, путем соединения четырех отрезков линий образуется прямоугольная форма. Треугольник можно получить, соединив отрезки по три линии и так далее.

Посмотрите на приведенную ниже схему, которая представляет различные двухмерные и трехмерные геометрические фигуры.

Двумерные геометрические фигуры

Давайте узнаем о пяти основных двумерных геометрических фигурах.

• Треугольник: Треугольник представляет собой замкнутую двумерную геометрическую форму с тремя сторонами. Например, эскиз кусочка пиццы, формы начос и т. д.
• Квадрат: Квадрат представляет собой двумерную геометрическую фигуру, образованную четырьмя сторонами одинаковой длины. Например, формы шахматной доски и карромной доски.
• Прямоугольник: прямоугольник представляет собой четырехстороннюю двумерную геометрическую фигуру, в которой длины противоположных сторон равны. Например, экраны ноутбуков и т. д.
• Круг: Круг представляет собой замкнутую двухмерную геометрическую фигуру круглой формы. Круг не имеет ни линий, ни углов. Например, основа для пиццы, колесо и т. д.
• Овал: Овал похож на круг, но его форма слегка вытянута. Овал не имеет прямых линий и углов. Например, форма числа ноль (0).

Трехмерные геометрические фигуры

Давайте теперь познакомимся с шестью основными трехмерными геометрическими фигурами.

• Куб: Куб представляет собой трехмерную геометрическую фигуру, состоящую из шести квадратов с равными сторонами. Например, игральные кости, кубик Рубика и т. д.
• Кубоид: кубоид — это трехмерная геометрическая фигура, состоящая из шести прямоугольников. Например, книга, коробка и т. д.
• Цилиндр: Цилиндр — это твердая трехмерная геометрическая фигура, имеющая два одинаковых круглых плоских конца. Например, банки с прохладительными напитками, лапша для бассейна и т. д.
• Сфера: Сфера — это сплошная трехмерная геометрическая форма, похожая на шар. Например, футбол, баскетбол и т. д.
• Полушарие: Полушарие — это геометрическая фигура, которая составляет половину сферы. Например, тарелки для супа.
• Конус: Конус представляет собой трехмерную геометрическую форму с плоским круглым основанием и заостренным краем наверху, называемым вершиной. Например, рожки для мороженого, клоунские шляпы и т. д.

Список и свойства геометрических фигур

Существует множество основных геометрических фигур, которые можно сформировать. Некоторые из них двумерные, а некоторые трехмерные. Список геометрических фигур вместе с их гранями, ребрами и вершинами приведен ниже:

Название	Тип	Края	Вершины	Лица
Квадрат	2D	4	4	—
Прямоугольник	2D	4	4	—
Треугольник	2D	3	3	—
Круг	2D	Изогнутый	0	—
Пентагон	2D	5	5	—
Шестигранник	2D	6	6	—
Куб	3D	12	8	6
Прямоугольный	3Д	12	8	6
Конус	3D	1	1	2
Цилиндр	3D	2	0	3
Сфера	3D	Изогнутый	0	1

► Похожие статьи

• Кольцо
• Усеченный конус
• Трапеция
• Параллелограмм

 

Примеры геометрических фигур

1. Пример 1: Приведите список геометрических фигур с двумя примерами из жизни.

   Решение: Ниже приведен список геометрических фигур с примерами из жизни:

   Список 2D геометрических фигур:

   • Треугольник: квадрат, дорожные знаки
   • Квадрат: клавиши виртуальной клавиатуры, шахматная доска
   • Прямоугольник: банкнота доллара, карты UNO
   • Круг: Алфавит O, обеденные тарелки
   • Овал: глаза человека, орбита Земли вокруг Солнца.

   Список трехмерных геометрических фигур:

   • Куб: кости, кубики льда
   • Кубовидный: кирпичи, тряпка
   • Цилиндр: прямые трубы, соломинки
   • Сфера: апельсины, баскетбол
   • Полусфера: миски, иглу
   • Конус: колпачки для вечеринок, воронка

2. Пример 2: Ответьте на следующие вопросы, исходя из своего понимания геометрических фигур.

   а) Я круглой формы (2D) без прямых линий и с одной полностью плоской поверхностью. Кто я?
   б) Я замкнутая двумерная фигура, образованная тремя прямыми линиями. Кто я?

   Решение:

   а) Окружность: Окружность представляет собой двумерную геометрическую фигуру с нулевым количеством прямых линий и одной полной круглой плоской поверхностью.
   б) Треугольник: Треугольник представляет собой двумерную геометрическую фигуру с тремя прямыми линиями.

3. Пример 3: Запишите количество прямых линий в следующих геометрических фигурах.
   а) Треугольник
   б) прямоугольник
   в) Квадрат
   г) Круг

   Решение:

   а) Треугольник: Треугольник состоит из трех прямых линий.
   б) Прямоугольник: прямоугольник состоит из четырех прямых линий.
   в) Квадрат: Квадрат состоит из четырех прямых линий. Все четыре линии равны.
   г) Круг: Круг не имеет прямых линий. Он круглой формы.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по геометрическим фигурам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о геометрических фигурах

Что такое геометрические фигуры в геометрии?

Геометрические фигуры также известны как геометрические фигуры, состоящие из комбинации линий или кривых. В реальной жизни нас окружают геометрические фигуры, например, окна в форме квадратов или двери в форме прямоугольников и т. д.

Какие существуют типы геометрических фигур?

Существуют два типа геометрических фигур: двухмерные и трехмерные геометрические фигуры. Двумерные фигуры — это замкнутые фигуры с длиной и шириной, такие как квадрат и прямоугольник. Трехмерные фигуры также являются замкнутыми фигурами, имеющими длину, ширину и высоту, например параллелепипед и куб.

Является ли прямая геометрической фигурой?

Прямая линия — это одномерная геометрическая фигура, имеющая только длину. Когда много прямых линий соединяются вместе, они образуют фигуры, такие как квадраты, треугольники и т. д.

Что такое трехмерные геометрические фигуры?

В геометрии трехмерная геометрическая фигура представляет собой объемную фигуру или форму с тремя измерениями: длиной, шириной и высотой. Например, цилиндр, сфера, параллелепипед и т. д.

Что такое двумерные геометрические фигуры?

Двумерная геометрическая фигура — это форма, которая имеет длину и ширину, но не имеет высоты или глубины. Круг, квадрат, прямоугольник, треугольник — вот несколько примеров двумерной формы.

Как называются геометрические фигуры?

Ниже приведен список некоторых основных геометрических фигур:

• Треугольник
• Прямоугольник
• Куб
• Прямоугольный
• Сфера
• Квадрат
• Ромб
• Трапеция

Какие основные геометрические фигуры?

Существует множество геометрических фигур в зависимости от их размеров. Круг, треугольник, квадрат, прямоугольник — вот лишь некоторые из основных двумерных фигур. Куб, прямоугольный параллелепипед, сфера, конус и цилиндр — вот лишь некоторые из основных трехмерных фигур или форм.

Каковы примеры основных геометрических фигур в реальной жизни?

Ниже перечислены несколько примеров геометрических фигур из реальной жизни:

• Круг: печенье, колеса велосипеда
• Квадрат: квадратная плитка на полу, квадратные бумажные салфетки
• Прямоугольник: учебники, сотовые телефоны, телеэкран
• Треугольник: сэндвич разрез по диагонали, дорожные знаки

Какая польза от геометрических фигур?

Геометрические формы освежают наши зрительные чувства логичным, практичным и интересным способом. Они придают ощущение порядка и аккуратности как работе, так и повседневной жизни.

Почему геометрические фигуры важны для детей?

Изучение геометрических фигур помогает детям идентифицировать визуальную информацию, а также помогает им в организации и обучении навыкам в различных областях. Дети развивают навыки распознавания лиц и навигации, если они могут классифицировать и сравнивать различные формы.

Скачать БЕСПЛАТНО учебные материалы

Рабочие листы по геометрическим фигурам

Что такое геометрические фигуры? Определение, типы, свойства, факты

Геометрические фигуры Определение

Геометрические фигуры — это замкнутые фигуры, созданные с использованием точек, отрезков, окружностей и кривых. Такие формы можно увидеть повсюду вокруг нас.

Примерами геометрических фигур являются круг, прямоугольник, треугольник и т. д. Пицца круглая, а ее ломтики треугольные. Точно так же двери и окна являются примерами прямоугольников.

У правильной формы все стороны равны. Например, квадрат или правильный шестиугольник. Неправильные формы имеют стороны разной величины. Например, разносторонний треугольник.

Некоторые из наиболее популярных фигур описаны ниже:

1. Прямоугольник

Прямоугольник — это форма, которая получается в результате соединения четырех разных точек четырьмя разными линиями. В прямоугольнике противоположные стороны параллельны и равны по длине. Все углы в прямоугольнике прямые. Отличие прямоугольника от квадрата в том, что в прямоугольнике два параллельных отрезка длиннее двух других, а в квадрате все отрезки имеют одинаковую длину.

Примерами прямоугольных объектов являются экраны ноутбуков, мобильные экраны и т. д.

2. Квадрат

Квадрат — это четырехсторонняя геометрическая фигура, образованная соединением четырех отрезков прямой равной длины. Подобно прямоугольнику, отрезки, образующие квадрат, лежат под прямым углом друг к другу. Примерами квадратных объектов являются кубик Рубика, игральные кости, шахматные доски и т. д.

3. Круг

Круг — это геометрическая фигура, состоящая из прямых линий. Можно считать, что окружность составлена ​​из бесчисленных точек, расположенных на одинаковом расстоянии от центральной точки.

Примерами круглых объектов являются целые пиццы и колеса.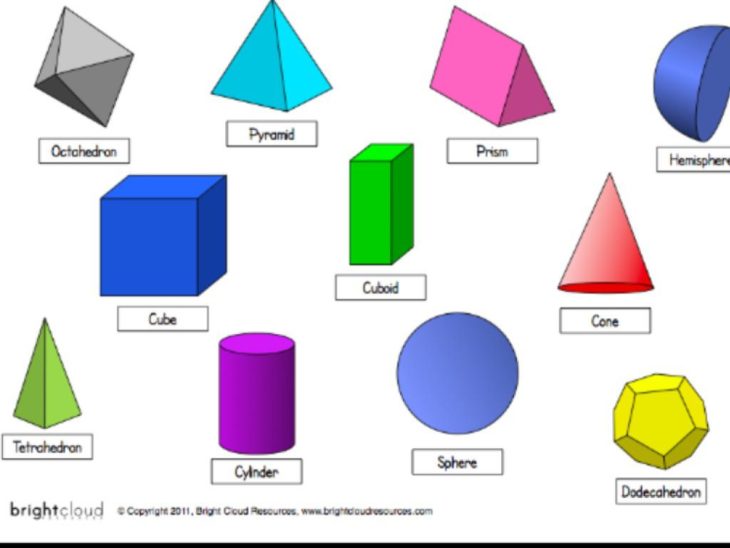

4. Треугольник 

Треугольник состоит из трех соединенных отрезков. Это сложная геометрическая фигура, поскольку она может иметь переменные углы и размеры.

Примерами треугольных объектов являются кусочки пиццы, начос, праздничные шапочки и т. д.

Примечательно, что название треугольника меняется в зависимости от его углов и размера сторон. Например, когда два отрезка треугольника образуют прямой угол, такой треугольник называется прямоугольным. Вот как это выглядит:

Любой треугольник с углами меньше 90 градусов называется остроугольным. Точно так же треугольник с одним углом больше 90 градусов называется тупоугольным треугольником. В равноугольном треугольнике все внутренние углы равны 60 градусов, а все стороны равны по длине. Обратитесь к диаграмме ниже, чтобы лучше понять.

Применение геометрических фигур в реальной жизни

Геометрия — это изучение формы и пространства. Это помогает нам понять другие математические концепции, а также приложения в реальной жизни. Геометрию можно использовать для проектирования зданий, мостов, автомобилей и даже одежды. Принципы геометрии также используются в других разделах математики, таких как тригонометрия и исчисление.

Ниже приведены некоторые из реальных применений:

Квадраты: Квадраты можно найти в природе, например, кристаллы квадратной формы. Квадраты также используются в искусстве. Ярким примером является известная картина Пита Мондриана «Композиция с красным, синим и желтым».

Прямоугольники: Многие искусственные объекты, такие как телевизоры, книги и компьютерные мониторы, имеют прямоугольную форму. Есть много реальных примеров прямоугольников, таких как банкноты, сотовые телефоны и обложки книг.

Круги: Круги можно увидеть повсюду вокруг нас, от пиццы, которую мы едим, до циферблата часов.

Треугольники: Треугольники можно найти во многих местах. Большинство крыш имеют треугольную форму, называемую фронтонами. Треугольники могут помочь поддерживать такие конструкции, как мосты и здания. Есть даже некоторые чипы, которые имеют форму треугольников.

Овалы/эллипсы: Овал или эллипс представляет собой вытянутый круг (яйцевидной формы), длина которого больше ширины.

Примеры трехмерных фигур

Трехмерные фигуры представляют собой группу вершин, линии, соединяющие вершины, и грани, заключенные в эти линии. Они имеют длину, ширину и высоту и занимают некоторый объем. Для многих трехмерных фигур грани двумерны. Кроме того, некоторые фигуры в трех измерениях имеют криволинейные поверхности.

В трех измерениях основными фигурами являются:

• Кубик: Кубик Рубика, кубик сахара
• Конус: Конус для мороженого, пирамидка
• Прямоугольный куб: Деревянная прямоугольная коробка, спичечный коробок
• Цилиндр: Рулон туалетной бумаги; банка газировки
• Сфера: Футбол, Баскетбол

Решаемые примеры 

Пример 1. Сколько сторон у десятиугольника?

Решение : У десятиугольника десять сторон и десять вершин.

Пример 2: Как называется треугольник, у которого только две равные стороны?

Решение : Треугольник, у которого только две равные стороны, называется равнобедренным.

Пример 3: конус имеет двумерную или трехмерную форму?
Решение : Конус представляет собой трехмерную фигуру.

Практические задачи

1

Квадрат имеет _________.

Две равные стороны

Четыре равные стороны

Четыре неравные стороны

Ни одна из этих

Правильный ответ: Четыре равные стороны
Квадрат в геометрии — это плоская фигура, имеющая четыре равные стороны и четыре прямых угла.

2

Расстояние от центра круга до его внешней границы называется _________.

радиус

кривая

диаметр

хорда

Правильный ответ: радиус
Расстояние от центра круга до его внешней границы называется радиусом круга. Диаметр круга всегда вдвое больше его радиуса.

3

Куб – это _________.

одномерная фигура

трехмерная фигура

двумерная фигура

Ничего из перечисленного

Правильный ответ: трехмерная фигура
Куб – это трехмерная фигура. У него шесть граней, восемь вершин и двенадцать ребер. Каждая грань куба представляет собой квадрат, и все ребра имеют одинаковую длину. У куба шесть квадратных граней.

4

Равносторонний треугольник _________.

открытая форма

неправильная форма

правильная форма

замкнутая кривая

Правильный ответ: правильная форма
Стороны равностороннего треугольника имеют одинаковую длину. Итак, равносторонний треугольник – это правильная фигура.